贵州省贵阳市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 已知 是关于x的一元二次方程 的一个根,则m的值是( )A、 B、0 C、1 D、0或12. 如图,在 中, ,若 ,则 的值为( )
 A、 B、 C、 D、3. 如图,水杯的杯口与投影面平行,投影线的几方向如箭头所示,它的正投影是( )
A、 B、 C、 D、3. 如图,水杯的杯口与投影面平行,投影线的几方向如箭头所示,它的正投影是( ) A、
A、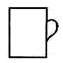 B、
B、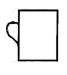 C、
C、 D、
D、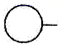 4. 如图, 在正方形网格中,下列正方形网格中的阴影图形与 相似的是( )
4. 如图, 在正方形网格中,下列正方形网格中的阴影图形与 相似的是( ) A、
A、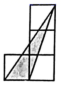 B、
B、 C、
C、 D、
D、 5. 如图,将菱形纸片 折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形 的边长为4, ,则 的值是( )
5. 如图,将菱形纸片 折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形 的边长为4, ,则 的值是( ) A、 B、2 C、 D、46. 小明将贵州健康码打印在面积为 的正方形纸上,如图所示为了估计图中健康码部分的面积,在纸内随机掷点,经过大量重复试验,发现点落入健康码部分的频率稳定在0.6左右,据此可以估计健康码部分的面积约为( )
A、 B、2 C、 D、46. 小明将贵州健康码打印在面积为 的正方形纸上,如图所示为了估计图中健康码部分的面积,在纸内随机掷点,经过大量重复试验,发现点落入健康码部分的频率稳定在0.6左右,据此可以估计健康码部分的面积约为( ) A、 B、 C、 D、7. 如图,图①是一个对角线长分别是6和8的菱形,将其沿对角线剪成四个全等的三角形,把这四个三角形无重叠地拼成如图②所示的大正方形,则图②中小正方形的面积为( )
A、 B、 C、 D、7. 如图,图①是一个对角线长分别是6和8的菱形,将其沿对角线剪成四个全等的三角形,把这四个三角形无重叠地拼成如图②所示的大正方形,则图②中小正方形的面积为( ) A、1 B、2 C、4 D、68. 已知反比例函数 与一次函数叫 的图象没有交点,则k的值可以是( )A、 B、 C、 D、9. 如图,正方形 的边长为3,点P为对角线 上任意一点, , ,垂足分别是E,Q,则 的值是( )
A、1 B、2 C、4 D、68. 已知反比例函数 与一次函数叫 的图象没有交点,则k的值可以是( )A、 B、 C、 D、9. 如图,正方形 的边长为3,点P为对角线 上任意一点, , ,垂足分别是E,Q,则 的值是( ) A、 B、3 C、 D、10. 如图,在长为10的线段 上,作如下操作:经过点B作 ,使得 ;连接 ,在 上截取 ;在 上截取 ,则 的长为( )
A、 B、3 C、 D、10. 如图,在长为10的线段 上,作如下操作:经过点B作 ,使得 ;连接 ,在 上截取 ;在 上截取 ,则 的长为( ) A、 B、 C、 D、11. 2020年12月29日,贵阳轨道交通2号线实现试运行,从白云区到观山湖区轨道公司共设计了132种往返车票,则这段线路有多少个站点?设这段线路有x个站点,根据题意,下面列出的方程正确的是( )A、 B、 C、 D、12. 如图,是一个正六棱柱的主视图和左视图,则图中x的值为( )
A、 B、 C、 D、11. 2020年12月29日,贵阳轨道交通2号线实现试运行,从白云区到观山湖区轨道公司共设计了132种往返车票,则这段线路有多少个站点?设这段线路有x个站点,根据题意,下面列出的方程正确的是( )A、 B、 C、 D、12. 如图,是一个正六棱柱的主视图和左视图,则图中x的值为( )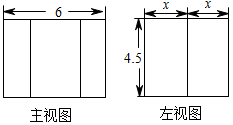 A、2 B、3 C、 D、
A、2 B、3 C、 D、二、填空题
-
13. 一元二次方程 的解是.14. 如图,在 中, ,若 与 的边 与 的比是 ,则它们的面积比为.
 15. 已知反比例函数 的图象具有下列特征:在每一象限内,y的值随x值的增大而减小,则m的取值范围是.16. 如图,以 的斜边 为边,向外作正方形 ,设正方形的对角线 与 的交点为O,连接 ,若 , ,则 的值是.
15. 已知反比例函数 的图象具有下列特征:在每一象限内,y的值随x值的增大而减小,则m的取值范围是.16. 如图,以 的斜边 为边,向外作正方形 ,设正方形的对角线 与 的交点为O,连接 ,若 , ,则 的值是.
三、解答题
-
17. 如图,用一条长为 的绳子围成矩形 ,设边 的长为 .
 (1)、直接写出 的长和矩形 的面积(用代数式表示)(2)、矩形 的面积是否可以是 ?请给出你的结论,并用所学知识说明理由.18. 一个蓄水池装满了水,蓄水池的排水速度 是排完水池中的水所用时间 的反比例函数,其图象如图所示.
(1)、直接写出 的长和矩形 的面积(用代数式表示)(2)、矩形 的面积是否可以是 ?请给出你的结论,并用所学知识说明理由.18. 一个蓄水池装满了水,蓄水池的排水速度 是排完水池中的水所用时间 的反比例函数,其图象如图所示.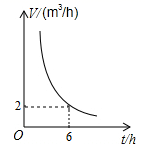 (1)、求出该蓄水池的蓄水量;(2)、若要在 (包括 和 )将水池的水排完,请求出排水速度的范围.19. 为参加我市开展“国家安全教育日”活动的知识竞赛,某校准备选出一个班代表学校参赛,甲班与乙班是学校两个实力相当的班级,让他们连续进行三场比赛,每场比赛都分出胜负后,获胜两场的班级将代表学校参赛,若甲班已经胜了第一场,请用列表或画树状图的方法,求出甲班能代表学校参赛的概率.20. 如图,已知四边形 是平行四边形,E是 延长线上一点且 ,连接 , .
(1)、求出该蓄水池的蓄水量;(2)、若要在 (包括 和 )将水池的水排完,请求出排水速度的范围.19. 为参加我市开展“国家安全教育日”活动的知识竞赛,某校准备选出一个班代表学校参赛,甲班与乙班是学校两个实力相当的班级,让他们连续进行三场比赛,每场比赛都分出胜负后,获胜两场的班级将代表学校参赛,若甲班已经胜了第一场,请用列表或画树状图的方法,求出甲班能代表学校参赛的概率.20. 如图,已知四边形 是平行四边形,E是 延长线上一点且 ,连接 , .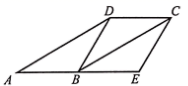 (1)、求证:四边形 是平行四边形(2)、连接 ,若 , ,求 的面积.21. 如图,已知小屋的高 ,小屋窗户的最低点G距离地面 ,某一时刻, 在阳光下的影长 ,在点A的正西方向 处选择点C,在此处拟建高为 的楼房 .(设点C、A、F在同一水平线上)
(1)、求证:四边形 是平行四边形(2)、连接 ,若 , ,求 的面积.21. 如图,已知小屋的高 ,小屋窗户的最低点G距离地面 ,某一时刻, 在阳光下的影长 ,在点A的正西方向 处选择点C,在此处拟建高为 的楼房 .(设点C、A、F在同一水平线上)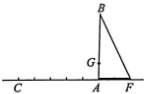 (1)、按比例较准确地画出楼房 及同一时刻它的影长;(2)、若楼房 建成后,请判断是否影响小屋的采光,并说明理由.
(1)、按比例较准确地画出楼房 及同一时刻它的影长;(2)、若楼房 建成后,请判断是否影响小屋的采光,并说明理由.

