广西壮族自治区贵港市港南区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. ﹣2的绝对值是( )A、﹣2 B、1 C、2 D、2. 函数 中,自变量 的取值范围是( )A、 B、 C、 且 D、 且3. 国家发改委2020年2月7日紧急下达第二批中央预算内投资2亿元人民币,专项补助承担重症感染患者救治任务的湖北多家医院重症治疗病区建设,其中数据2亿用科学记数法表示为( )A、2× B、2× C、20× D、0.2×4. 如果将一组数据5、4、6、5、4、13、5依次重复写10次,会得到70个数组成的一组新数据,关于这组新数据的中位数、众数、平均数,下列说法正确的是( )A、中位数是4 B、众数是10 C、中位数和众数都是5 D、中位数平均数都是55. 下列运算正确的是( )A、a+b=ab B、(x+1)2 =x2+1 C、a10÷ a5=a2 D、(﹣a3)2=a66. 若关于x的一元二次方程x2﹣2 x+m=0有两个实数根,则m的取值范围是( )A、m≥ B、m≤ C、m≥3 D、m≤37. 在平面直角坐标系中,将点 向下平移2个单位长度得到的点的坐标是( )A、 B、 C、 D、8. 下列命题中,假命题的是( )A、两条弧的长度相等,它们是等弧 B、等弧所对的圆周角相等 C、所有的等边三角形都相似 D、位似图形一定有位似中心9. 如图, 、 是 的半径, 是 上一点,连接 、 .若 ,则 的大小为( )
 A、126° B、116° C、108° D、106°10. 如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC= ,AC=3,则CD的长为( )
A、126° B、116° C、108° D、106°10. 如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC= ,AC=3,则CD的长为( )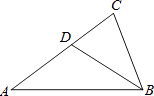 A、1 B、 C、2 D、11. 如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则EF ED的最小值为( )
A、1 B、 C、2 D、11. 如图,正方形ABCD的边长AB=8,E为平面内一动点,且AE=4,F为CD上一点,CF=2,连接EF,ED,则EF ED的最小值为( ) A、6 B、4 C、4 D、612. 如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°.其中正确的结论共有( )
A、6 B、4 C、4 D、612. 如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°.其中正确的结论共有( )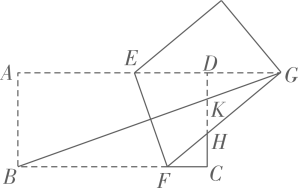 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 比较大小:3 4 .14. 已知x2+3x+5的值为3,则代数式3x2+9x−1的值为 .15. 某校对1000名女生身高进行了测量,身高在1.58-1.63(单位:m)这个小组的频率为0.25,则该组的人数为名.16. 如图,直线 , , ,点 在直线 上, ,若 ,则 的度数为.
 17. 如图一个扇形纸片的圆心角为90°,半径为4,将这张扇形纸片折叠,使点 与点 恰好重合,折痕为 ,则图中阴影部分的面积为.
17. 如图一个扇形纸片的圆心角为90°,半径为4,将这张扇形纸片折叠,使点 与点 恰好重合,折痕为 ,则图中阴影部分的面积为.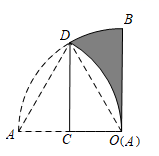 18. 如图,在平面直角坐标系中,点A1的坐标为(1,2),以点O为圆心,以OA1长为半径画弧,交直线 于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2 , 以O为圆心,以OA2长为半径画弧,交直线 于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3 , 以点O为圆心,以OA3长为半径画弧,交直线 于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4 , 以点O为圆心,以OA4长为半径画弧,交直线 于点B4 , …按照如此规律进行下去,点B2020的坐标为.
18. 如图,在平面直角坐标系中,点A1的坐标为(1,2),以点O为圆心,以OA1长为半径画弧,交直线 于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2 , 以O为圆心,以OA2长为半径画弧,交直线 于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3 , 以点O为圆心,以OA3长为半径画弧,交直线 于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4 , 以点O为圆心,以OA4长为半径画弧,交直线 于点B4 , …按照如此规律进行下去,点B2020的坐标为.
三、解答题
-
19.(1)、计算: .(2)、先化简,再求值 ,其中 为方程 的根.20. 如图,已知等腰三角形 的顶角 .
 (1)、在 上作一点 ,使 (要求:尺规作图,保留作图痕迹,不必写作法和证明).(2)、写出 的度数.21. 如图,一次函数 的图象分别交 轴、 轴于 , 两点,交反比例函数 图象于 , 两点.
(1)、在 上作一点 ,使 (要求:尺规作图,保留作图痕迹,不必写作法和证明).(2)、写出 的度数.21. 如图,一次函数 的图象分别交 轴、 轴于 , 两点,交反比例函数 图象于 , 两点. (1)、求直线 的表达式;(2)、点 是线段 上一点,若 ,求 点的坐标.22. 学校随机对本校部分学生进行“假期中,我在家可以这么做: .扎实学习、 .快乐游戏、 .经典阅读、 .分担劳动、 .乐享健康”网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中信息,回答下列问题.
(1)、求直线 的表达式;(2)、点 是线段 上一点,若 ,求 点的坐标.22. 学校随机对本校部分学生进行“假期中,我在家可以这么做: .扎实学习、 .快乐游戏、 .经典阅读、 .分担劳动、 .乐享健康”网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中信息,回答下列问题. (1)、这次调查的总人数是人;(2)、请补全条形统计图,并求扇形统计图中 所对应的圆心角;(3)、若该学校共有学生1700人,则选择 有多少人?23. 汽车产业是我市支柱产业之一,产量和效益逐年增加.据统计,2008年我市某种品牌汽车的年产量为64万辆,到2010年,该品牌汽车的年产量达到100万辆.若该品牌汽车年产量的年平均增长率从2008年开始五年内保持不变.(1)、求年平均增长率;(2)、求该品牌汽车2011年的年产量为多少万辆?24. 如图,在 中,点 为 边上一点,连接 .以 为直径作 .恰好经过点 ,过点 作 的平行线交 延长线于点 ,交 于点 .
(1)、这次调查的总人数是人;(2)、请补全条形统计图,并求扇形统计图中 所对应的圆心角;(3)、若该学校共有学生1700人,则选择 有多少人?23. 汽车产业是我市支柱产业之一,产量和效益逐年增加.据统计,2008年我市某种品牌汽车的年产量为64万辆,到2010年,该品牌汽车的年产量达到100万辆.若该品牌汽车年产量的年平均增长率从2008年开始五年内保持不变.(1)、求年平均增长率;(2)、求该品牌汽车2011年的年产量为多少万辆?24. 如图,在 中,点 为 边上一点,连接 .以 为直径作 .恰好经过点 ,过点 作 的平行线交 延长线于点 ,交 于点 . (1)、若 ,求证: 是 的切线.(2)、在(1)的条件下,若 , ,求 的半径.25. 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,4),B点在y轴上.
(1)、若 ,求证: 是 的切线.(2)、在(1)的条件下,若 , ,求 的半径.25. 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,4),B点在y轴上.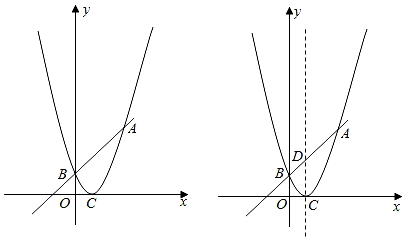 (1)、求m的值及这个二次函数的解析式;(2)、若P是线段AB下方抛物线上一动点,当△ABP面积最大时,求P点坐标以及△ABP面积最大值;(3)、若D为直线AB与这个二次函数图象对称轴的交点,Q为线段AB之间的一个动点,过Q作x轴的垂线,与这个二次函数图象交于点E,问是否存在这样的点Q,使得四边形DCEQ为平行四边形,若存在,请求出Q点的坐标;若不存在,请说明理由.26. 如图,在平面直角坐标系中,已知矩形 的顶点 在 轴上,顶点 在 轴上, , ,点 为对角线 上一动点,过点 作 , 交 轴于点 .
(1)、求m的值及这个二次函数的解析式;(2)、若P是线段AB下方抛物线上一动点,当△ABP面积最大时,求P点坐标以及△ABP面积最大值;(3)、若D为直线AB与这个二次函数图象对称轴的交点,Q为线段AB之间的一个动点,过Q作x轴的垂线,与这个二次函数图象交于点E,问是否存在这样的点Q,使得四边形DCEQ为平行四边形,若存在,请求出Q点的坐标;若不存在,请说明理由.26. 如图,在平面直角坐标系中,已知矩形 的顶点 在 轴上,顶点 在 轴上, , ,点 为对角线 上一动点,过点 作 , 交 轴于点 .
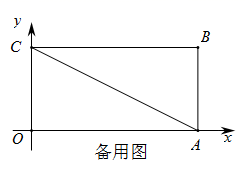 (1)、 ;(2)、在点 从点 运动到点 的过程中, 的值是否发生变化?如果变化,请求出其变化范围;如果不变,请求出其值;(3)、若将 沿直线 折叠后,点 与点 重合,请求出 的长为多少?
(1)、 ;(2)、在点 从点 运动到点 的过程中, 的值是否发生变化?如果变化,请求出其变化范围;如果不变,请求出其值;(3)、若将 沿直线 折叠后,点 与点 重合,请求出 的长为多少?