广西壮族自治区崇左市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

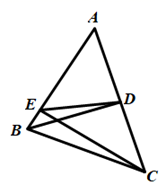
1. 已知 $\sin α = \frac{\sqrt{3}}{2} ， α$ 是锐角，则 $∠ α$ 的度数是（）

A、30° B、45° C、60° D、90°

查看试题解析
2. 二次函数 $y = 2 - {(x + 1)}^{2}$ 的顶点坐标是（）

A、 $(1 ， 2)$ B、 $(- 1 ， 2)$ C、 $(2 ， - 1)$ D、 $(- 1 ， - 2)$

查看试题解析
3. 在同一直角坐标系中，关于 $y = x^{2} ， y = x^{2} + 2 ， y = - 2 x^{2} - 1$ 的图象，说法正确的是（）

A、开口方向相同 B、都经过原点 C、都关于y轴对称 D、互相可以通过平移得到

查看试题解析
4. 如果5x=6y，那么下列结论正确的是（）

A、 $x : 6 = y : 5$ B、 $x : 5 = y : 6$ C、 $x = 5, y = 6$ D、 $x = 6, y = 5$

查看试题解析
5. 如图，E是平行四边形ABCD的BA边的延长线上的一点，CE交AD于点F．下列各式中，错误的是（）.

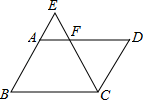A、 $\frac{A E}{A B} = \frac{A F}{B C}$ B、 $\frac{A E}{A B} = \frac{A F}{D F}$ C、 $\frac{A E}{A B} = \frac{F E}{F C}$ D、 $\frac{A E}{B E} = \frac{A F}{B C}$

查看试题解析
6. 关于直角三角形，下列说法正确的是（）

A、所有的直角三角形一定相似 B、如果直角三角形的两边长分别是3和4，那么第三边的长一定是5 C、如果已知直角三角形两个元素（直角除外），那么这个直角三角形一定可解 D、如果已知直角三角形一锐角的三角函数值，那么这个直角三角形的三边之比一定确定

查看试题解析
7. 若 $R (x_{1}, y_{1}), P (x_{2}, y_{2})$ 是函数 $y = - \frac{5}{x}$ 图像上的两点，当 $x_{1} > x_{2} > 0$ 时，下列结论正确的是（）

A、 $y_{2} > y_{1} > 0$ B、 $y_{1} > y_{2} > 0$ C、 $y_{2} < y_{1} < 0$ D、 $y_{1} < y_{2} < 0$

查看试题解析
8. 已知在 $R t △ A B C$ 中， $∠ C = 90 ° ， A B = 7 ， B C = 5$ ，则下列式子中正确的是（）

A、 $\sin A = \frac{5}{7}$ B、 $\sin B = \frac{5}{7}$ C、 $\tan A = \frac{2 \sqrt{6}}{5}$ D、 $\tan A = \frac{5}{7}$

查看试题解析
9. 如图，在矩形 $A B C D$ 中， $E$ 是 $B C$ 的中点，连接 $A E$ ，过点E作 $E F ⊥ A E$ 交 $D C$ 于点 $F$ .若 $A B = 4 ， B C = 6$ ，则 $D F$ 的长为（）

A、 $\frac{9}{4}$ B、 $\frac{7}{4}$ C、 $\sqrt{3}$ D、1

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 ° ， A D ⊥ B C$ 于点 $D$ ，若 $B D ： C D = 3 ： 2$ ，则 $\tan ∠ D A C$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{6}}{3}$ C、 $\frac{\sqrt{6}}{2}$ D、 $\frac{\sqrt{15}}{3}$

查看试题解析
11. 如图，在△ABC中，D，E分别是AB，AC上的点，且DE// BC，若AE： EC=1： 4，那么 $S_{△ A D E} ： S_{△ B E C}$ 的值为（）

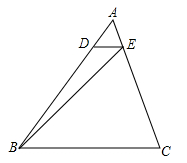A、1∶16 B、1∶18 C、1∶20 D、1∶24

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，下列结论：① $a b c > 0$ ；② $9 a + c > 0$ ；③ $a x^{2} + b x + c = 0$ 的两个根是 $x_{1} = - 2 ， x_{2} = 4$ ；④ $b ： c = 1 ： 4$ 其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 对于函数 $y = \frac{2 m - 1}{x}$ ，当 $x > 0$ 时，y随x的增大而减小，则m的取值范围是.

查看试题解析
14. 某人从地面沿着坡度为 $i = 1 : \sqrt{3}$ 的山坡走了 $100$ 米，这时他离地面的高度是米．

查看试题解析
15. 已知抛物线y₁＝a（x﹣m）²+k与y₂＝a（x+m）²+k（m≠0）关于y轴对称，我们称y₁与y₂互为“和谐抛物线”．请写出抛物线y＝﹣4x²+6x+7的“和谐抛物线” ．

查看试题解析
16. 如图，在平行四边形 $A B C D$ 中，点 $E$ 在 $B C$ 边上，且 $C E ： B E = 2 ： 1$ ， $A C$ 与 $D E$ 相交于点 $F$ ；若 $S_{△ A F D} = 9$ ，则 $S_{△ C F E} =$ .

查看试题解析
17. 如果抛物线 $y = a x^{2} - 3 x + 1$ 与x轴有交点，那么a的取值范围是.

查看试题解析
18. 如图，点 $P$ 是双曲线 $C$ ： $y = \frac{4}{x}$ （ $x > 0$ ）上的一点，过点 $P$ 作 $x$ 轴的垂线交直线 $A B$ ： $y = \frac{1}{2} x - 2$ 于点 $Q$ ，连结 $O P$ ， $O Q$ .当点 $P$ 在曲线 $C$ 上运动，且点 $P$ 在 $Q$ 的上方时，△ $P O Q$ 面积的最大值是.

查看试题解析

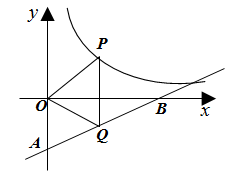
三、解答题

19. 计算 $\sqrt{3} \cos 30 ° + 2^{- 1} - \sqrt{2} \sin 45 ° - {(\tan 60 ° + 1)}^{0}$

查看试题解析
20. 如图，已知正比例函数 $y = 2 x$ 与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象交于 $A$ ， $B$ 两点，且点 $A$ 的横坐标 $x$ 为4，若 $C$ 的坐标为 $(0 ， 8)$ ，连接 $A C ， B C$ .

求：

(1)、反比例函数的解析式；

(2)、观察图象，直接写出不等式 $2 x < \frac{k}{x}$ 的解集；

(3)、求 $△ A B C$ 的面积.

查看试题解析
21. 在如图的方格纸中， $△ O A B$ 的顶点坐标分别为 $O (0 ， 0) ， A (- 2 ， - 1) ， B (- 1 ， - 3)$ ， $△ O_{1} A_{1} B_{1}$ 与 $△ O A B$ 是关于点 $P$ 为位似中心的位似图形.

（1）在图中标出位似中心 $P$ 的位置，并写出点 $P$ 及点 $B$ 的对应点 $B_{1}$ 的坐标；
（2）以原点 $O$ 为位似中心，在位似中心的同侧画出 $△ O A B$ 的一个位似 $△ O A_{2} B_{2}$ ，使它与 $△ O A B$ 的位似比为2∶1，并写出点B的对应点 $B_{2}$ 的坐标.

查看试题解析
22. 如图，已知在△ABC中，点D是BC边上一点，DA⊥AB，AC=12，BD=7，CD=9.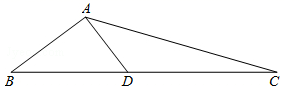

(1)、求证：△ACD∽△BCA；

(2)、求tan∠CAD的值.

查看试题解析
23. 已知：如图，斜坡 $A P$ 的坡度为1∶2.4，坡长 $A P$ 为260米，在坡顶A处的同一水平面有一座古塔 $B C$ ，在斜坡底P处测得该塔的塔顶的仰角为 $45 °$ ，在坡顶A处测得该塔的塔顶的仰角为 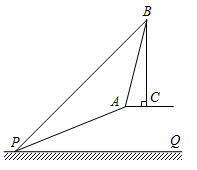$76 °$ .

求：

(1)、坡顶到地面 $P O$ 的距离；

(2)、古塔 $B C$ 的高度（结果精确到1米）.
（参考数据 $\sin 76 ° \approx 0.97 ， \cos 76 ° \approx 0.24 ， \tan 76 ° \approx 4.01$ ）

查看试题解析
24. 某汽车经销商购进A，B两种型号的低排量汽车，其中A型汽车的进货单价比B型汽车的进货单价多2万元，经销商花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相等.销售中发现A型汽车的每周销量 $y_{A}$ （台）与售价x（万元/台）满足函数关系式 $y_{A} = - x + 20$ ，B型汽车的每周销量 $y_{B}$ （台）与售价x（万元/台）满足函数关系式 $y_{B} = - x + 14$ .

(1)、求A，B两种型号的汽车的进货单价；

(2)、已知A型汽车的售价比B型汽车的售价高2万元/台，设B型汽车售价为t万元/台.每周销售这两种车的总利润为W万元，求W与t的函数关系式，A，B两种型号的汽车售价各为多少时，每周销售这两种车的总利润最大？最大总利润是多少万元？

查看试题解析
25. 如图，在△ABC中，BD、CE是△ABC的高，连接DE．

(1)、求证： $△ ABD$ ∽ $△ ACE$ ；

(2)、若∠BAC＝60°，BC＝ $6 \sqrt{2}$ ，求DE的长．

查看试题解析
26. 如图，已知抛物线y＝ax²﹣2x+c经过△ABC的三个顶点，其中点A(0，1)，点B(9，10)，AC∥x轴．

(1)、求这条抛物线的解析式.

(2)、求tan∠ABC的值.

(3)、若点D为抛物线的顶点，点E是直线AC上一点，当△CDE与△ABC相似时，求点E的坐标．

查看试题解析