广西河池市环江县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
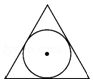
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 若关于 的方程 有实数根,则 的取值范围是( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、 C、
C、 D、
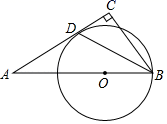
D、 4. 二次函数y=﹣3(x+1)2﹣7有( )A、最大值﹣7 B、最小值﹣7 C、最大值7 D、最小值75. 将抛物线 向右平移1个单位,再向上平移3个单位后,它的解析式为( )A、 B、 C、 D、6. 下列事件是随机事件的是( )A、购买一张福利彩票就中奖 B、有一名运动员奔跑的速度是50米 秒 C、在一个标准大气压下,水加热到 会沸腾 D、在一个仅装有白球和黑球的袋中摸球,摸出红球7. 如图,AB是⊙O的直径,AC=BC,则∠A的度数等于( )
4. 二次函数y=﹣3(x+1)2﹣7有( )A、最大值﹣7 B、最小值﹣7 C、最大值7 D、最小值75. 将抛物线 向右平移1个单位,再向上平移3个单位后,它的解析式为( )A、 B、 C、 D、6. 下列事件是随机事件的是( )A、购买一张福利彩票就中奖 B、有一名运动员奔跑的速度是50米 秒 C、在一个标准大气压下,水加热到 会沸腾 D、在一个仅装有白球和黑球的袋中摸球,摸出红球7. 如图,AB是⊙O的直径,AC=BC,则∠A的度数等于( )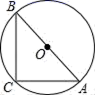 A、30° B、45° C、60° D、90°8. 一个布袋里装有2个红球、3个黄球和5个白球,除颜色外其它都相同.搅匀后任意摸出一个球,是黄球的概率为( )A、 B、 C、 D、9. 已知圆心角是 ,半径为30的扇形的弧长为( )A、 B、 C、 D、10. 已知圆心角为 的扇形的弧长为 ,该扇形的面积为( )A、 B、 C、 D、11. 已知直线 经过一、二、三象限,则抛物线 大致是( )A、
A、30° B、45° C、60° D、90°8. 一个布袋里装有2个红球、3个黄球和5个白球,除颜色外其它都相同.搅匀后任意摸出一个球,是黄球的概率为( )A、 B、 C、 D、9. 已知圆心角是 ,半径为30的扇形的弧长为( )A、 B、 C、 D、10. 已知圆心角为 的扇形的弧长为 ,该扇形的面积为( )A、 B、 C、 D、11. 已知直线 经过一、二、三象限,则抛物线 大致是( )A、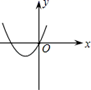 B、
B、 C、
C、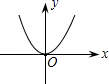 D、
D、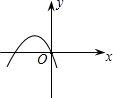 12. 如图, 的半径为 , ,则经过点 的弦长可能是( )
12. 如图, 的半径为 , ,则经过点 的弦长可能是( )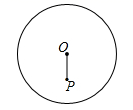 A、3 B、5 C、9 D、12
A、3 B、5 C、9 D、12二、填空题
-
13. 一元二次方程 的根是 .14. 抛物线y=﹣x2+2x﹣5与y轴的交点坐标为.15. 数学老师将全班分成4个小组开展合作学习,采用随机抽签方式确定2个小组进行展示活动,则第1小组和第2小组被抽到的概率是.16. 已知在半径为3的 中,弦 的长为4,那么圆心 到 的距离为.
 17. 如图,在边长为 的正六边形 中, 是 的中点,则 .
17. 如图,在边长为 的正六边形 中, 是 的中点,则 .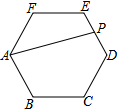 18. 如图,在平面直角坐标系 中,已知点 , 为平面内的动点,且满足 , 为直线 上的动点,则线段 长的最小值为.
18. 如图,在平面直角坐标系 中,已知点 , 为平面内的动点,且满足 , 为直线 上的动点,则线段 长的最小值为.
三、解答题
-
19. 解方程:20.
 (1)、画图:图①为正方形网格,画出 绕点 顺时针旋转 后的图形.(2)、尺规作图:在图②中作出四边形 关于点 对称的图形(不写作法,保留作图痕迹,用黑色笔将作图痕迹涂黑).21. 已知 是关于 的二次函数, , 满足下表
(1)、画图:图①为正方形网格,画出 绕点 顺时针旋转 后的图形.(2)、尺规作图:在图②中作出四边形 关于点 对称的图形(不写作法,保留作图痕迹,用黑色笔将作图痕迹涂黑).21. 已知 是关于 的二次函数, , 满足下表x
…
-1
0
1
3
…
y
…
0
0.75
1
0
…
观察上表(不用求解析式),直接写出该函数如下性质:
(1)、图象函数名称 , 开口方向;(2)、对称轴表达式;(3)、顶点坐标;(4)、 随 的变化情况 , .22. 如图1,点 表示我国古代水车的一个盛水筒.如图2,当水车工作时,盛水筒的运行路径是以轴心 为圆心, 为半径的圆.若 被水面截得的弦 长为 ,求水车工作时,盛水筒在水面以下的最大深度.
 23.
23.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
 24. 某电脑销售店电脑原价为每台5000元,元旦期间开展了促销活动,将原价经过两次下调后,促销价为每台4050元.(1)、求平均每次下调的百分率;(2)、某校计划以促销价购买100台电脑.该店还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送12个月的免费保修费,免费保修费为每台每月10元.请问哪种方案更优惠?
24. 某电脑销售店电脑原价为每台5000元,元旦期间开展了促销活动,将原价经过两次下调后,促销价为每台4050元.(1)、求平均每次下调的百分率;(2)、某校计划以促销价购买100台电脑.该店还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送12个月的免费保修费,免费保修费为每台每月10元.请问哪种方案更优惠?