山东省东营市广饶县2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、 ${(\sqrt{3})}^{2} =9$ B、 $\sqrt{25} = \pm 5$ C、 $\sqrt[3]{- 8} = 2$ D、 $\sqrt{36} = 6$

查看试题解析
3. 在地球某地，地表以下岩层的温度y（℃）与所处深度x（km）之间的关系可以近似地用表达式y=35x+20来表示，当自变量x每增加1km时，因变量y的变化情况是（）

A、减少35℃ B、增加35℃ C、减少55℃ D、增加55℃

查看试题解析
4. 一次函数 $y = k x + b (k \neq 0)$ 在平面直角坐标系内的图像如图所示，则k和b的取值范围是（）

A、 $k > 0$ ， $b > 0$ B、 $k < 0$ ， $b < 0$ C、 $k < 0$ ， $b > 0$ D、 $k > 0$ ， $b < 0$

查看试题解析
5. 如图小敏做了一个角平分仪ABCD，其中AB= AD，BC= DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD ，使它们分别落在角的两边上，过点A、C画一条射线AE，AE就是∠PRQ的平分线。此角平分仪的画图原理是（）

A、SSS B、SAS C、ASA D、AAS

查看试题解析
6. 如图，若“马”所在的位置的坐标为（-2，-1），“象”所在位置的坐标为（-1，1），则“兵”所在位置的坐标为（）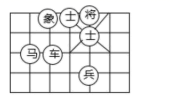

A、（-2，1） B、（-2，2） C、（1，-2） D、（2，-2）

查看试题解析
7. 如图，长方体的长为15宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（）

A、20 B、25 C、30 D、32

查看试题解析
8. 下列判断：①一个数的平方根等于它本身，这个数是 $0$ 和 $1$ ；②实数包括无理数和有理数；③ $2$ 的算术平方根是 $\sqrt{2}$ ；④无理数是带根号的数．正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
9. 一列货运火车从A出发，匀加速行驶一段时间后开始匀速行驶，过了一段时间，火车到达下一个车站停下，装完货后，火车又匀加速行驶，一段时间后再次开始匀速行驶，那么可以近似的刻画出火车在这段时间内的速度变化情况的是（）

A、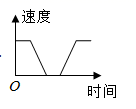 B、 C、 D、

查看试题解析
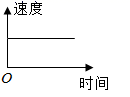10. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧，分别交AB、AC于点M、N，再分别以M、N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，下列结论：①AD是 $∠ B A C$ 的平分线；②∠ADB=120°；③DB=2CD；④若CD=4， $A B = 8 \sqrt{3}$ ，则△DAB的面积为20．其中正确的结论共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 如果P(m+3，2m+4)在y轴上，那么点P的坐标是.

查看试题解析
12. 如图， $A B = A C$ ，要使 $△ A B E ≌ △ A C D$ ，依据 $A S A$ ，应添加的一个条件是.

查看试题解析
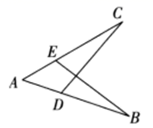13. 如图，点P是△ABC内一点，∠ABC=80°，∠1=∠2，则∠BPC=度．

查看试题解析
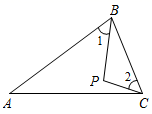14. 如图，长方形ABCD的边AD长为2，AB长为1，点A在数轴上对应的数是-1，以A点为圆心，对角线AC长为半径画弧，交数轴于点E，点E表示的实数是．

查看试题解析
15. 如图是温度计的示意图，左边的刻度表示摄氏温度，右边的刻度表示华氏温度，华氏温度y（℉）与摄氏温度x（℃）之间的函数关系式为．

查看试题解析
16. 若实数m、n满足等式 $| m - 2 | + \sqrt{n - 4} = 0$ ，且m、n恰好是等腰△ABC的两条边的边长，则△ABC的周长是．

查看试题解析
17. 如图，在平面直角坐标系中，已知点 $A (0 ， 4)$ ， $B (2 ， 4)$ ，直线 $y = \frac{1}{2} x + 1$ 上有一动点 $P$ ，当 $P A = P B$ 时，点 $P$ 的坐标是．

查看试题解析
18. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2）…按这样的运动规律经过第2021次运动后，动点P的坐标是．

查看试题解析

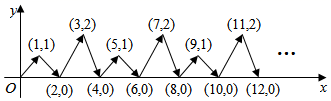
三、解答题

19. 计算：

(1)、 $\sqrt[3]{- 27} + \sqrt{3} - 6 - (- \sqrt{3})$ ；

(2)、 ${(- 1)}^{2021} - \sqrt[3]{8} + | \sqrt{3} - 2 | + {(- \frac{1}{2})}^{- 2}$ ．

查看试题解析
20. 在8×8的方格纸中，设小方格的边长为1．

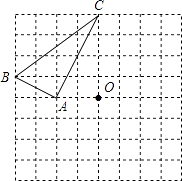(1)、请判断△ABC的形状并说明理由．

(2)、画出△ABC以CO所在直线为对称轴的对称图形△A′B′C′，并在所画图中标明字母．

查看试题解析
21. 尺规作图：
已知： $Δ A B C$ .求作： $Δ A^{'} B^{'} C^{'}$ ，使 $Δ A^{'} B^{'} C^{'}$ 与 $Δ A B C$ 全等.

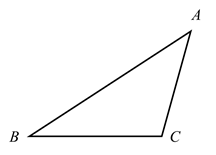
要求：

①不写作法，保留作图痕迹；

②写出作图时选取的相等的边或角.

查看试题解析
22. 如图，点A的坐标为（3，0），以点A为圆心，5个单位长度为半径画圆，分别交x轴于点B、C，交y轴于点E、F．求点B、C、E、F的坐标．

查看试题解析
23. 某电信公司手机的A类收费标准如下：不管通话时间多长，每部手机每月必须缴月租费12元，另外，通话费按0.2元/min计；B类收费标准如下：没有月租费，但通话费按0.3元/min计．按照此类收费标准完成下列各题：

(1)、直接写出每月应缴费用y（元）与通话时长x（分）之间的关系式：A类：；B类：

(2)、若每月平均通话时长为300分钟，选择类收费方式较少．

(3)、求每月通话多长时间时，按 A．B两类收费标准缴费，所缴话费相等．

查看试题解析
24. 如图，已知AB=CD，∠B=∠C，AC和BD交于点O，OE⊥AD于点E．

(1)、△AOB与△DOC全等吗?请说明理由；

(2)、若OA=3，AD=4，求△AOD的面积．

查看试题解析
25. 已知，在△ABC中，∠BAC=90°，AB=AC，点D为BC的中点．

(1)、观察猜想如图①，若点E、F分别为AB、AC上的点，且DE⊥DF于点D，则线段BE与AF的数量关系式是（不需要说明理由）；

(2)、类比探究如图②，若点E、F分别为AB、CA延长线上的点，且DE⊥DF于点D，请写出BE与AF的数量关系式，并说明理由；

(3)、解决问题如图③，点M在AD的延长线上，点N在AC上，且∠BMN=90°，若AM=2，AN=1，则AB的长为．

查看试题解析
26. 如图，已知直线y=﹣2x+8与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．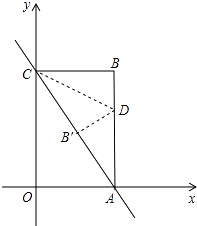

(1)、求点A、C的坐标；

(2)、将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式；

(3)、在（2）的条件下，坐标平面内是否存在点P（除点B外），使得△APC与△ABC全等？若存在，直接写出符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析