吉林省长春市宽城区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. -8的绝对值等于（）

A、8 B、 $- 8$ C、 $- \frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
2. 2020年某市各级各类学校学生人数约为1 580 000人，将1 580 000 这个数用科学记数法表示为（）

A、0.158×10⁷ B、15.8×10⁵ C、1.58×10⁶ D、1.58×10⁷

查看试题解析
3. 下列图形是四棱柱的侧面展开图的是（）

A、 B、 C、 D、

查看试题解析
4. 有理数a在数轴上的对应点的位置如图所示，若有理数b满足-a＜b＜a，则b的值不可能是（）

A、2 B、0 C、-1 D、-3

查看试题解析
5. 数M精确到0.01时，近似数是2.90，那么数M的范围是（）

A、2.8≤M<3 B、2.80≤M≤3.00 C、2.85≤M<2.95 D、2.895≤M<2.905

查看试题解析
6. 如图，AB和CD相交于点O，则下列结论正确的是（）

A、∠1=∠2 B、∠2=∠3 C、∠3=∠4 D、∠1=∠5

查看试题解析
7. 如图，下列说法中错误的是（）

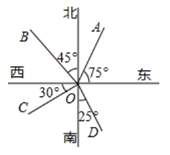A、OA方向是北偏东15° B、OB方向是西北方向 C、OC方向是南偏西30° D、OD方向是南偏东25°

查看试题解析
8. 如图，给出下列条件：①∠1=∠2；②∠3=∠4；③∠B=∠DCE；④∠B+∠BAD=180°，其中能推出 $A B // C D$ 的是（）

A、①② B、①③ C、②③ D、②④

查看试题解析

二、填空题

9. 长春市净月潭国家森林公园门票的价格为成人票每张30元，儿童票每张15元．若购买m张成人票和n张儿童票，则共需花费元．

查看试题解析
10. 若单项式x^a+2y³与 $\frac{1}{4}$ x⁶y³是同类项，则a的值是．

查看试题解析
11. 把多项式 $\frac{3}{2} x^{2} + \frac{5}{3} - 3 x + \frac{1}{2} x^{3}$ 按x的升幂排列为．

查看试题解析
12. 如图，某单位要在河岸 $l$ 上建一个水泵房引水到C处，他们的做法是：过点C作 $C D ⊥ l$ 于点D，将水泵房建在了D处．这样做最节省水管长度，其数学道理是．

查看试题解析
13. 如图，O是线段AB的中点，点C在线段AB上．若AB=15，BC=2AC，则线段OC的长为．

查看试题解析
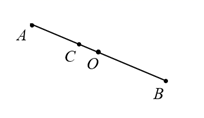14. 如图， $A B // C D$ ，点M为CD上一点，MF平分∠CME．若∠1＝57°，则∠EMD的大小为度．

查看试题解析

三、解答题

15. 计算：

(1)、 $(- 8) \times (- 10) + 12 \div (- 6)$ ；

(2)、 $- 3^{2} - 25 \times {(- \frac{2}{5})}^{2}$ ；

(3)、 $3 m^{2} n - 4 m n^{2} - 3 + 5 m^{2} n + 2 m n^{2} + 5$ ；

(4)、 $2 (3 x^{2} - y^{2}) - 3 (2 y^{2} - 3 x^{2})$ .

查看试题解析
16. 如图， $D E // B C ， E F // A B$ ，图中与∠BFE互补的角有几个，请分别写出来．

查看试题解析
17. 先化简，再求值： $3 (2 x^{2} - 4 x y + \frac{1}{3} y^{2}) - 2 (x^{2} - 6 x y + y^{2})$ ，其中 $x = - \frac{1}{2}, y = \frac{4}{3}$ ．

查看试题解析
18. 某校准备围建一个长方形花圃，其中一边靠墙，墙足够长，另外三边用长为30 米的篱笆围成．设花圃垂直于墙的一边长为x 米．

(1)、用含x的代数式表示花圃的面积．

(2)、当x=5时，求花圃的面积．

查看试题解析
19. 如图，点P是∠AOB的边OB上的一点，点M是∠AOB内部的一点，按下述要求画图，并回答问题：

(1)、过点M画OA的平行线MN；

(2)、过点P画OB的垂线PC，交OA于点C；

(3)、点C到直线OB的距离是线段的长度．

查看试题解析
20. 如图， $A D // B C$ ，∠1=∠C，∠B=60°，DE平分∠ADC交BC于点E，
试说明 $A B // D E$ ．请完善解答过程，并在括号内填写相应的理论依据．

解：∵ $A D // B C$ ，（已知）

∴∠1=∠=60°．（）

∵∠1=∠C，（已知）

∴∠C=∠B=60°．（等量代换）

∵ $A D // B C$ ，（已知）

∴∠C+∠=180°．（）

∴∠=180°-∠C=180°-60°=120°．（等式的性质）

∵DE平分∠ADC，（已知）

∴∠ADE= $\frac{1}{2}$ ∠ADC= $\frac{1}{2}$ ×120°=60°．（）

∴∠1=∠ADE．（等量代换）

∴ $A B // D E$ ．（）

查看试题解析
21. 如图，点C是线段AB的中点，点D是线段CB上的一点，点E是线段DB的中点，AB=20，EB=3．

(1)、求线段DB的长．

(2)、求线段CD的长．

查看试题解析
22. 如图，点O为直线AB上一点，过点O作射线OC，使∠AOC=3∠BOC，将含30°角的直角三角板的直角顶点放在点O处．

(1)、将直角三角板按图①的位置放置，使ON在射线OA上，OM在直线AB的下方，则∠AOC＝度，∠MOC＝度．

(2)、将直角三角板按图②的位置放置，使OM在射线OA上，ON在直线AB的上方，试判断∠CON与∠BOC的大小关系，并说明理由．

查看试题解析
23. 数学中，运用整体思想方法在求代数式的值时非常重要．
例如：已知a²＋2a＝2，则代数式2a²＋4a＋3＝2（a²＋2a）＋3＝2×2＋3＝7．

请你根据以上材料解答以下问题：

(1)、若 $x^{2} - 3 x = 4$ ，求 $1 - x^{2} + 3 x$ 的值．

(2)、当x＝1时，代数式px³＋qx－1的值是5，求当x＝－1时，代数式px³＋qx－1的值．

(3)、当x＝2020时，代数式ax⁵＋bx³＋cx＋6的值为m，直接写出当 $x = - 2020$ 时，代数式ax⁵＋bx³＋cx＋6的值．（用含m的代数式表示）

查看试题解析
24. 如图， $A M / / B N$ ，∠A＝60°．点P是射线AM上一动点（与点A不重合），BC平分∠ABP交AM于点C，BD平分∠PBN交AM于点D．

(1)、求∠ABN的度数．

(2)、求∠CBD的度数．

(3)、当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若变化，请写出变化规律；若不变化，请写出它们之间的数量关系，并说明理由．

查看试题解析