吉林省长春市朝阳区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 若有理数a与3互为相反数，则a的值是（）.

A、3 B、－3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 下图是由5个大小相同的正方体组成的立体图形，其俯视图是（）

A、 B、 C、 D、

查看试题解析
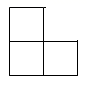3. 《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数若收入80元记作+80元，则 $- 50$ 元表示 $($ $)$

A、收入50元 B、收入30元 C、支出50元 D、支出30元

查看试题解析
4. 若一个整数12500…0用科学记数法表示为1.25×10¹⁰ ，则原数中“0”的个数为（　　）

A、5 B、8 C、9 D、10

查看试题解析
5. 如图，直线 $b$ 、 $c$ 被直线 $a$ 所截，则 $∠ 1$ 与 $∠ 2$ 是（）

A、内错角 B、同位角 C、同旁内角 D、对顶角

查看试题解析
6. 下列代数式中，次数为3的单项式是（）

A、 $- a^{3} b$ B、 $3 a^{2} b^{2}$ C、 $4 a^{3} - 3$ D、 $\frac{x^{2} y}{4}$

查看试题解析
7. 如图，A点在B点的北偏东40°方向，C点在B点的北偏东75°方向，A点在C点的北偏西50°方向，则∠BAC的度数是（）

A、85° B、80° C、90° D、95°

查看试题解析
8. 如果 $M = x^{2} + 3 x + 12$ ， $N = - x^{2} + 3 x - 5$ ，那么M与N的大小关系是（）

A、 $M > N$ B、 $M < N$ C、 $M = N$ D、无法确定

查看试题解析

二、填空题

9. - $\frac{1}{5}$ 的绝对值是．

查看试题解析
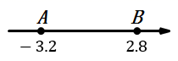
10. 如图，在数轴上，点A与点B之间表示整数的点有个．

查看试题解析
11. 若 $∠ 1 = 65 °$ ，则 $∠ 1$ 的补角的大小为°．

查看试题解析
12. 一个三位数，它的百位数字为a，十位数字为b，个位数字为c，则这个三位数可以表示为．

查看试题解析
13. 计算： $33 ° 52' + 21 ° 54' =$ ．

查看试题解析
14. 如图，在平面内，两条直线l₁ ， l₂相交于点O，对于平面内任意一点M，若p，q分别是点M到直线l₁ ， l₂ ，的距离，则称（p，q）为点M的“距离坐标”．根据上述规定，“距离坐标”是（3，2）的点共有个．

查看试题解析

三、解答题

15. 计算：

(1)、 $- 2^{3} \div 6 + {(- 1)}^{2020}$

(2)、 $1.5 - (- 4 \frac{1}{4}) + 3.75 - (+ 8 \frac{1}{2})$

查看试题解析
16. 以下是马小虎同学化简代数式 $(a^{2} b + 4 a b) - 3 (a b - a^{2} b)$ 的过程．

(1)、马小虎同学解答过程在第步开始出错，出错原因是．

(2)、请你帮助马小虎同学写出正确的解答过程．

查看试题解析
17. 已知：图①、图②、图③均为 $5 \times 3$ 的正方形网格，在网格中选择2个空白的正方形并涂上阴影，与图中的4个阴影正方形一起构成正方体表面展开图，且3种方法得到的展开图不完全重合．

查看试题解析
18. 如图， $A B = 10$ ，点C是线段AB的中点，点D是线段CB的中点，求AD的长．

查看试题解析
19. 先化简，再求值： $6 (x^{2} - 2 x) + 2 (1 + 3 x - 2 x^{2}) - 2 x^{2}$ ，其中 $x = \frac{1}{2}$ ．

查看试题解析
20. 补全下面的解题过程：

如图，已知OC是∠AOB内部的一条射线，OD是∠AOB的平分线，∠AOC＝2∠BOC且∠BOC＝40°，求∠COD的度数．

解：因为∠AOC＝2∠BOC，∠BOC＝40°，

所以∠AOC＝°，

所以∠AOB＝∠AOC+∠＝°．

因为OD平分∠AOB，

所以∠AOD＝ $\frac{1}{2}$ ∠＝°，

所以∠COD＝∠﹣∠AOD＝°．

查看试题解析
21. 如图， $A B / / C D$ ， $∠ B = 70 °$ ， $∠ B C E = 20 °$ ， $∠ C E F = 130 °$ ．

(1)、AB与EF的位置关系是

(2)、对（1）中判断的AB与EF的位置关系加以证明．

查看试题解析

22. 某市自2020年1月起，对餐饮用水开始实行阶梯式计量水价，该阶梯式计量水价分为三级（如下表所示）：

	月用水量（立方米）	水价（元/立方米）
第一级	50立方米以下（含50立方米）的部分	4.6
第二级	50立方米—150立方米（含150立方米）的部分	6.5
第三级	150立方米以上的部分	8

(1)、受疫情影响，某饭店4月份用水量为15立方米，则该饭店4月份需交的水费为元．

(2)、若某饭店9月份用水量为

a (50 \leq a \leq 150)

立方米，则该饭店9月份应交的水费为元（用含a的代数式表示）．

(3)、若某饭店11月份交水费1080元，求该饭店11月份的用水量．

查看试题解析

23. 如图

(1)、如图①， $A B / / C D$ ， $∠ P A B = 130 °$ ， $∠ P C D = 120 °$ ．求 $∠ A P C$ 的度数．
（提示：过点P作直线 $P Q / / A B$ ）

(2)、如图②， $A D / / B C$ ，点P在射线OM上运动， $∠ A D P = ∠ a$ ， $∠ B C P = ∠ β$ ．
①当点P在线段AB上运动时， $∠ C P D$ ， $∠ α$ ， $∠ β$ 之间的数量关系为．

②当点P在A，B两点外侧运动时（点P与点A，B，O三点不重合），直接写出 $∠ C P D$ ， $∠ a$ ， $∠ β$ 之间的数量关系为．

查看试题解析
24. 如图，A，B，C是数轴上三点，点B表示的数为4， $A B = 8$ ， $B C = 2$ ．

(1)、在数轴上，点A表示的数为，点C表示的数为．

(2)、动点P，Q分别从A，C同时出发，点P以每秒2个单位长度的速度沿数轴向右匀速运动，点Q以每秒1个单位长度的速度沿数轴向左匀速运动，设点P的运动时间为 $t (t > 0)$ ．
①在数轴上，点P表示的数为，点Q表示的数为（用含t的代数式表示）．

②若 $P B = 5 Q B$ ，则t= ．

查看试题解析