黑龙江省哈尔滨市香坊区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列实数中是无理数的是( )A、 B、 C、3.1 D、02. 下列方程是一元一次方程的是( )A、 B、 C、 D、3. 下列图案中,可由左侧图案平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图, 和 不是同旁内角的是( )A、
4. 如图, 和 不是同旁内角的是( )A、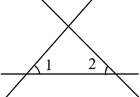 B、
B、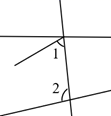 C、
C、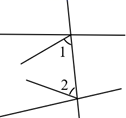 D、
D、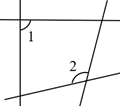 5. 已知x=y , 则下面变形错误的是( )A、x+a=y+a B、x-a=y-a C、2x=2y D、6. 甲、乙两人练习赛跑,甲每秒跑7m,乙每秒跑5m,甲让乙先跑8m,设甲出发x秒可追上乙,则可列方程为( )A、 B、 C、 D、7. 如图,已知平行线a,b,一个直角三角板的直角顶点在直线a上,另一个顶点在直线b上,若 ,则 的大小为( )
5. 已知x=y , 则下面变形错误的是( )A、x+a=y+a B、x-a=y-a C、2x=2y D、6. 甲、乙两人练习赛跑,甲每秒跑7m,乙每秒跑5m,甲让乙先跑8m,设甲出发x秒可追上乙,则可列方程为( )A、 B、 C、 D、7. 如图,已知平行线a,b,一个直角三角板的直角顶点在直线a上,另一个顶点在直线b上,若 ,则 的大小为( ) A、 B、 C、 D、8. 若点P在x轴上方,y轴的左侧,到每条坐标轴的距离都是6,则点P的坐标为( )A、(6,6) B、(﹣6,6) C、(﹣6,﹣6) D、(6,﹣6)9. 下列命题为假命题的是( )A、对顶角相等 B、如果 ,垂足为O,那么 C、经过一点,有且只有一条直线与这条直线平行 D、两直线平行,同位角相等10. 如图,下列条件:① ;② ;③ ;④ ,其中能判定 的是( )
A、 B、 C、 D、8. 若点P在x轴上方,y轴的左侧,到每条坐标轴的距离都是6,则点P的坐标为( )A、(6,6) B、(﹣6,6) C、(﹣6,﹣6) D、(6,﹣6)9. 下列命题为假命题的是( )A、对顶角相等 B、如果 ,垂足为O,那么 C、经过一点,有且只有一条直线与这条直线平行 D、两直线平行,同位角相等10. 如图,下列条件:① ;② ;③ ;④ ,其中能判定 的是( ) A、①② B、②③ C、①④ D、②④
A、①② B、②③ C、①④ D、②④二、填空题
-
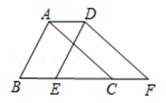
11. 的相反数是 .12. 已知 是一元一次方程,则 .13. 将点 向上平移2个单位长度得到点Q,则点Q的坐标为 .14. 比较大小: 4(填“ ”,“ ”或“ ”)15. 若点 在y轴上,则a的值是 .16. 姐姐比弟弟大3岁,若5年前姐姐的年龄是弟弟的2倍,则姐姐现在的年龄是岁.17. 在同一平面内,直线AB与直线CD相交于点O, ,射线 ,则 的度数为 .18. 如图,将周长为12的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为
 19. 一件商品标价140元,若八折出售,仍可获利12%,则这件商品的进价为元.20. 两个角的两边两两互相平行,且一个角的 等于另一个角的 ,则这两个角中较小角的度数为 .
19. 一件商品标价140元,若八折出售,仍可获利12%,则这件商品的进价为元.20. 两个角的两边两两互相平行,且一个角的 等于另一个角的 ,则这两个角中较小角的度数为 .三、解答题
-
21. 计算(1)、(2)、22. 解方程(1)、(2)、23. 如图,在正方形网格中建立平面直角坐标系,已知点 , , ,请按下列要求操作:

①请在图中画出 ;
②将 向上平移5个单位长度,再向左平移4个单位长度,得到 .在图中画出 ,并直接写出点 、 、 的坐标.
24. 已知:直线AB与直线CD交于点O,过点O作 .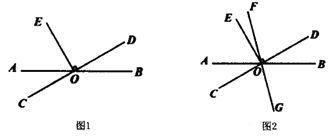 (1)、如图1,若 ,求 的度数;(2)、如图2,过点O画直线FG满足射线OF在 内部,且使 ,在不添加任何辅助线的情况下,请直接写出与 互余的角.25. 某超市计划购进甲、乙两种型号的节能灯共700只,若购进700只灯的进货款恰好为20000元,这两种节能灯的进价、预售价如下表:
(1)、如图1,若 ,求 的度数;(2)、如图2,过点O画直线FG满足射线OF在 内部,且使 ,在不添加任何辅助线的情况下,请直接写出与 互余的角.25. 某超市计划购进甲、乙两种型号的节能灯共700只,若购进700只灯的进货款恰好为20000元,这两种节能灯的进价、预售价如下表:型号
进价(元/只)
预售价(元/只)
甲型
20
25
乙型
35
40
(1)、求购进甲、乙两种型号的节能灯各多少只?(2)、超市按预售价将购进的甲型节能灯全部售出,购进的乙型节能灯部分售出后,决定将乙型节能灯打九折销售,全部售完后,两种节能灯共获利3100元,求乙型节能灯按预售价售出的数量是多少?26. 如图1是长方形纸带将长方形ABCD沿EF折叠成图2,使点C、D分别落在点 、 处,再沿BF折叠成图3,使点 、 分别落在点 、 处. (1)、若 ,求图1中 的度数;(2)、在(1)的条件下,求图2中 的度数;(3)、在图3中写出 、 与 的数量关系,并说明理由.27. 如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为 ,点B的坐标为 ,点C的坐标为 ,且m,n满足 .
(1)、若 ,求图1中 的度数;(2)、在(1)的条件下,求图2中 的度数;(3)、在图3中写出 、 与 的数量关系,并说明理由.27. 如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为 ,点B的坐标为 ,点C的坐标为 ,且m,n满足 . (1)、分别求点A、点C的坐标;(2)、P点从点C出发以每秒2个单位长度的速度向终点B匀速运动,连接AP,设点P的运动时间为t秒,三角形ABP的面积为s(平方单位),求s与t的关系式;(3)、在(2)的条件下,过点P作 轴交线段CA于点Q,连接BQ,当三角形BCQ的面积与三角形ABQ的面积相等时,求Q点坐标.
(1)、分别求点A、点C的坐标;(2)、P点从点C出发以每秒2个单位长度的速度向终点B匀速运动,连接AP,设点P的运动时间为t秒,三角形ABP的面积为s(平方单位),求s与t的关系式;(3)、在(2)的条件下,过点P作 轴交线段CA于点Q,连接BQ,当三角形BCQ的面积与三角形ABQ的面积相等时,求Q点坐标.