黑龙江省哈尔滨市松北区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列各式中,是一元一次方程的是( )A、 B、 C、 D、2. 下列各组图形可以通过平移互相得到的是( )A、
 B、
B、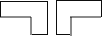 C、
C、 D、
D、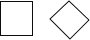 3. 下列各数,2, ,3.14, , , ,其中无理数共有( )A、2个 B、3个 C、4个 D、5个4. 在平面直角坐标系中,点 所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列等式的变形正确的是( )A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么6. 七年级学生人数为x,其中男生占52%,女生有150人,下列正确的是( )A、 B、 C、 D、7. 点 在直角坐标系的x轴上,则P点坐标为( )A、 B、 C、 D、8. 一个长方形的周长为26cm,若这个长方形的长减少3cm,就可成为一个正方形,设这个长方形的长为 ,可列方程( )A、 B、 C、 D、9.
3. 下列各数,2, ,3.14, , , ,其中无理数共有( )A、2个 B、3个 C、4个 D、5个4. 在平面直角坐标系中,点 所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列等式的变形正确的是( )A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么6. 七年级学生人数为x,其中男生占52%,女生有150人,下列正确的是( )A、 B、 C、 D、7. 点 在直角坐标系的x轴上,则P点坐标为( )A、 B、 C、 D、8. 一个长方形的周长为26cm,若这个长方形的长减少3cm,就可成为一个正方形,设这个长方形的长为 ,可列方程( )A、 B、 C、 D、9.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
 A、30° B、25° C、20° D、15°10. 甲计划用若干个工作日完成某项工作,从第二个工作日起,乙加入此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成此项工作的天数是( )A、8天 B、7天 C、6天 D、5天
A、30° B、25° C、20° D、15°10. 甲计划用若干个工作日完成某项工作,从第二个工作日起,乙加入此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成此项工作的天数是( )A、8天 B、7天 C、6天 D、5天二、填空题
-
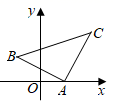
11. 的相反数是.12. 已知 是方程 的解,那么a的值是 .13. 比较大小:2 414. 把命题“对顶角相等”改写成“如果…那么…”的形式是.15. 当 时,点 在x轴上.16. 某商品进价为100元,按进价提高50%后标价,实际销售时给顾客打了八折,卖出这件商品的利润是 .17. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/小时,水速为2千米/时,则A港和B港相距千米.18. 如图所示,点 、B(-1,1)、 ,则 的面积是 .
 19. 已知点P的坐标为 ,且点P到两坐标轴的距离相等,则a的值为 .20. 如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,则∠EBA的度数为 .
19. 已知点P的坐标为 ,且点P到两坐标轴的距离相等,则a的值为 .20. 如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,则∠EBA的度数为 .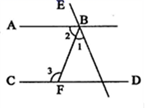
三、解答题
-
21. 计算:(1)、 ;(2)、 .22. 按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
 (1)、点A的坐标为;(2)、将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1 , 画出△A1B1C1 .(3)、△A1B1C1的面积为 .23. 解下列一元一次方程(1)、(2)、24. 完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
(1)、点A的坐标为;(2)、将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1 , 画出△A1B1C1 .(3)、△A1B1C1的面积为 .23. 解下列一元一次方程(1)、(2)、24. 完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.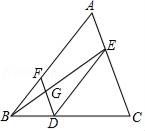
证明:∵DE∥AB(已知),
∴∠A=∠CED()
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD()
∴DF∥AE()
∴∠EGF+∠AEG=180°()
25. 某中学开学初到商场购买A.B两种品牌的额温枪,购买A种品牌的额温枪50个,B种品牌的额温枪25个,共花费4500元,已知购买一个B种品牌的额温枪比购买两个A种品牌的额温枪少花20元.(1)、如果购买一个A种品牌的额温枪a元,则购买一个B种品牌额温枪元(用含a的式了表示).(2)、求购买一个A种品牌的额温枪和一个B种品牌的额温枪各需多少元;(3)、由于疫情比预计的时间要长,学校决定第二次购买A、B两种品牌额温枪共50个.正好赶上商场对商品价格进行调整,A种品牌额温枪售价比第一次购买时提高了8%,B种品牌额温枪按第一次购买时售价的九折出售.如果学校第二次购买A、B两种品牌额温枪的总费用是第一次购买额温枪总费用的70%,求学校第二次购买A种品牌的额温枪多少个.26. 如图,直线CB∥OA , ∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB , OE平分∠COF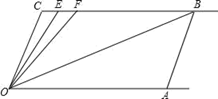 (1)、求∠EOB的度数;(2)、若平行移动AB , 那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)、在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.27. 如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+ =0,过C作CB⊥x轴于B.
(1)、求∠EOB的度数;(2)、若平行移动AB , 那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)、在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.27. 如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+ =0,过C作CB⊥x轴于B.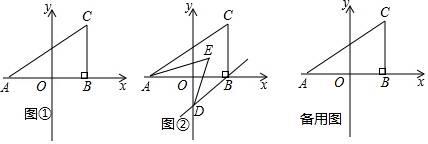 (1)、求三角形ABC的面积;(2)、如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;(3)、在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
(1)、求三角形ABC的面积;(2)、如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;(3)、在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.