黑龙江省大庆市肇源县(五四学制)2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列计算中,结果是 的是( )A、 B、 C、 D、2. 如图,下列推理错误的是( )
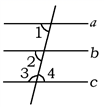 A、∵ , B、∵ C、 D、∵3. 变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )A、13 B、5 C、2 D、3.54. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )
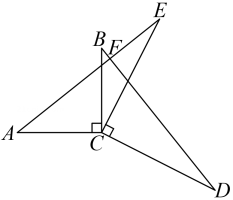
A、∵ , B、∵ C、 D、∵3. 变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )A、13 B、5 C、2 D、3.54. 花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①、②、③、④),若要配一块与原来大小一样的三角形玻璃,应该带( )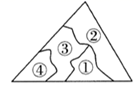 A、第①块 B、第②块 C、第③块 D、第④块5. 如图,点 是直线 外一点, , , , 都在直线上, 于 ,下列线段最短的是( )
A、第①块 B、第②块 C、第③块 D、第④块5. 如图,点 是直线 外一点, , , , 都在直线上, 于 ,下列线段最短的是( )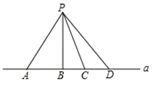 A、 B、 C、 D、6. 如图,AB=AC,添加下列条件,不能使△ABE≌△ACD的是( )
A、 B、 C、 D、6. 如图,AB=AC,添加下列条件,不能使△ABE≌△ACD的是( )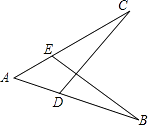 A、∠B=∠C B、∠AEB=∠ADC C、AE=AD D、BE=DC7. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分拼成一个长方形(无重叠部分),通过计算两个图形中阴影部分的面积,可以验证的一个等式是( )
A、∠B=∠C B、∠AEB=∠ADC C、AE=AD D、BE=DC7. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分拼成一个长方形(无重叠部分),通过计算两个图形中阴影部分的面积,可以验证的一个等式是( )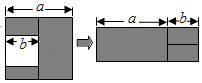 A、a2﹣b2=(a+b)(a﹣b) B、a(a﹣b)=a2﹣ab C、(a﹣b)2=a2﹣2ab+b2 D、a(a+b)=a2+ab8. 小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系( )A、
A、a2﹣b2=(a+b)(a﹣b) B、a(a﹣b)=a2﹣ab C、(a﹣b)2=a2﹣2ab+b2 D、a(a+b)=a2+ab8. 小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系( )A、 B、
B、 C、
C、 D、
D、 9. 如图,已知∠O ,点 P 为其内一定点,分别在∠O 的两边上找点 A 、 B ,使△ PAB 周长最小的是( )A、.
9. 如图,已知∠O ,点 P 为其内一定点,分别在∠O 的两边上找点 A 、 B ,使△ PAB 周长最小的是( )A、.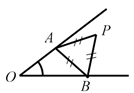 B、
B、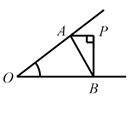 C、
C、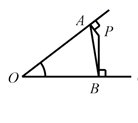 D、
D、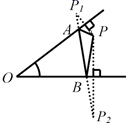 10. 在 中, , ,D为BC中点,E,F分别是AB,AC两边上的动点,且 ,下列结论:① ;② 的长度不变;③ 的度数不变;④四边形AEDF的面积为 .其中正确的结论个数是( )
10. 在 中, , ,D为BC中点,E,F分别是AB,AC两边上的动点,且 ,下列结论:① ;② 的长度不变;③ 的度数不变;④四边形AEDF的面积为 .其中正确的结论个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 某种秋冬流感病毒的直径约为 米, 用科学记数法表示为 .12. 已知a、b满足 ,则 .13. 若多项式 是完全平方式,则 的值是 .14. 用直尺和圆规作一个角等于已知角的示意图如图,则要说明 ,需要证明 ≌ ,则这两个三角形全等的依据是(写出全等的简写理由)
 15. 两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 .16. 如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为 三角形ACE的面积为y,则y与x的关系式为.
15. 两条直线相交所构成的四个角,其中:①有三个角都相等;②有一对对顶角相等;③有一个角是直角;④有一对邻补角相等,能判定这两条直线垂直的有 .16. 如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为 三角形ACE的面积为y,则y与x的关系式为.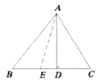 17. 如图,三角形纸片ABC,AB=11cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为cm.
17. 如图,三角形纸片ABC,AB=11cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为cm.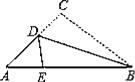 18. 如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是 .
18. 如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是 . 19. 填空:把下面的推理过程补充完整,并在括号内注明理由.
19. 填空:把下面的推理过程补充完整,并在括号内注明理由.已知:如图, , , ,试说明 .

解: 已知
▲ ( ▲ )
在 与 中
≌ ( ▲ )
( ▲ )
三、解答题
-
20. 计算: .21. 计算:22. 先化简,再求值: ,其中 .23. 利用乘法公式计算:24. 如图,点P是 外一点,点M、N分别是 两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若 , , ,则线段QR的长为多少 .
 25. “十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).(1)、求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;(2)、当x=280(千米)时,求剩余油量Q的值;(3)、当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.26. 如图,点A、C、D、B在同一条直线上,且
25. “十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).(1)、求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;(2)、当x=280(千米)时,求剩余油量Q的值;(3)、当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.26. 如图,点A、C、D、B在同一条直线上,且 (1)、求证:(2)、若 ,求 的度数.
(1)、求证:(2)、若 ,求 的度数.