北京市延庆区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. $- 8$ 的相反数是（）

A、 $\frac{1}{8}$ B、 $- 8$ C、 $8$ D、 $- \frac{1}{8}$

查看试题解析
2. 2020年6月23日，北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道，它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成.该卫星距离地面约36000千米，将数据36000用科学记数法表示为（）

A、 $3.6 \times 10^{3}$ B、 $3.6 \times 10^{4}$ C、 $3.6 \times 10^{5}$ D、 $36 \times 10^{4}$

查看试题解析
3. 一实验室检测A、B、C、D四个元件的质量（单位：克），超过标准质量的克数记为正数，不足标准质量的克数记为负数，结果如图所示，其中最接近标准质量的元件是（）

A、 B、 C、 D、

查看试题解析
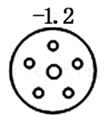
4. 如图所示的圆柱体从正面看得到的图形可能是（）

A、 B、 C、 D、

查看试题解析
5. 如图，数轴上有A，B，C，D四个点，其中所对应的数的绝对值最大的点是（）

A、点A B、点B C、点C D、点D

查看试题解析
6. 下列方程中，解为x=4的方程是（）.

A、x-1=4 B、4x=1 C、4x-1=3x+3 D、2（x-1）=1

查看试题解析
7. 下列运算结果正确的是（）

A、5x﹣x=5 B、2x²+2x³=4x⁵ C、﹣4b+b=﹣3b D、a²b﹣ab²=0

查看试题解析
8. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托．”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺．则正确的方程是（）

A、 $\frac{1}{2} x = (x - 5) - 5$ B、 $\frac{1}{2} x = (x + 5) + 5$ C、 $2 x = (x - 5) - 5$ D、 $2 x = (x + 5) + 5$

查看试题解析

二、填空题

9. 用四舍五入法将533.625精确到个位，所得到的近似数为．

查看试题解析
10. 写出单项式－a³b的一个同类项：．

查看试题解析
11. 如图1，在直线MN的异侧有A，B两点，要在直线MN上取一点C，使AC+BC最短．小明的作法是连接线段AB交直线MN于点C，如图2．这样作图得到的点C，就使得AC+BC最短，依据是．

查看试题解析
12. 如果|a－2|+（b+3）²=0，那么a+b= ．

查看试题解析
13. 如图的流程图是小明解方程3x＋1＝x－3的过程．其中③代表的运算步骤为系数化1，该步骤对方程进行变形的依据是．

查看试题解析
14. 代数式3x²－4x的值为7，那么6x²－8x－9的值为．

查看试题解析
15. 已知，∠AOB=50°，∠BOC＝30°，OD是∠AOC的角平分线，则∠DOB的度数是．

查看试题解析
16. 计算（+2）+（－5）的思考过程如下：
a．决定应用有理数加法法则中“异号的两个数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值”；

b．确定和的符号：计算出加数+2和－5的绝对值，分别是2和5，通过比较它们的绝对值发现，加数－5的绝对值较大，写出和的符号为“－”；

c．确定和的绝对值：5－2=3；

d．写出计算结果－3；

e．判断出是两个有理数相加的问题；

f．观察两个加数的符号，发现是异号两数相加．

请你仔细阅读以上思考过程，写出正确的顺序：．

查看试题解析

三、解答题

17. 计算：

(1)、 $(- 4) + (- 8) - (+ 2)$

(2)、 $(- 36) \div (+ 12) - (- 4) \times (- \frac{1}{2})$

(3)、 $(\frac{1}{6} + \frac{1}{2} - \frac{7}{8}) \times (- 24)$

查看试题解析
18. 解方程：

(1)、 $3 (x - 5) = - 17$

(2)、 $\frac{5 - x}{3} - \frac{x}{4} = \frac{x - 1}{2}$

查看试题解析
19. 解不等式： $3 (x + 1) \leq 5 x + 7$ ，并把它的解集在数轴上表示出来．

查看试题解析
20. 先化简，再求值：
$3 (x^{2} - x y) - 2 (x^{2} - y^{2}) + 3 x y$ ，其中 $x = - 1$ ， $y = 3$ ．

查看试题解析
21. 如图

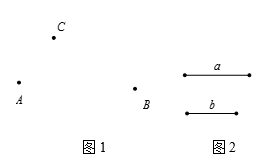(1)、如图1，平面上有3个点A，B，C．
①画直线AB；画射线BC；画线段AC；

②过点C作AB的垂线，垂足为点D；

③量出点C到直线AB的大约距离．

(2)、尺规作图：
已知：线段a，b，如图2．

求作：一条线段MN，使它等于2a－b．（不写作法，保留作图痕迹）

查看试题解析
22. 根据要求作答

(1)、如图，OC平分∠AOB，∠AOC=40°．求∠BOC的度数．

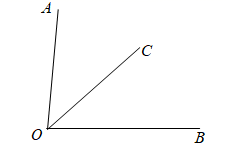(2)、如图，点O是直线AB上的一点，∠1与∠2互余，求∠DOC的度数．

(3)、如图，点C是线段AB的中点，AD=6，BD=4，求CD的长．

查看试题解析
23. 列方程解应用题：
晚饭后，小明的爸爸像往常一样去散步．半小时后，妈妈发现爸爸没有带手机，就让小明骑自行车去给爸爸送手机．如果爸爸的速度是4千米/时，小明骑自行车的速度是12千米/时，小明用多少时间可以追上爸爸？（要求：先写出审题过程，在设未知数列方程）

查看试题解析
24. 已知，点O是数轴的原点，点A、点B是数轴上不重合的两个点，且点A在点B的左边，点M是线段AB的中点．在上述条件下，解决问题：

(1)、如果点A表示的数是4，点B表示的数是6，那么点M表示的数是；

(2)、如果点A表示的数是－3，点M表示的数是2，那么点B表示的数是；

(3)、如果点A表示的数是a，点B表示的数是b，那么点M表示的数是；（用含a，b的代数式表示），所以AM=BM．因此得到关于x的方程：x－a=b－x．

(4)、解出这个方程：x－a=b－x．

(5)、如果点A表示的数是－2，点C表示的数是3，点B是线段OC上的一点，点M表示的数为m，则m的取值范围是；

(6)、如果点E表示的数是1，点F表示的数是x，点A从点E出发，以每分钟1个单位长度的速度向右运动，点B从点F出发，以每分钟3个单位长度的速度向右运动，设运动时间为t（t＞0）．

①当x=5时，如果EM=6，求t的值；

②当t≤3时，如果EM≤9，求x的取值范围．

查看试题解析
25. 阅读材料：
如果x是一个有理数，我们把不超过x的最大整数记作[x] ．

例如，[3.2]=3，[5]=5，[－2.1]=－3．

那么，x=[x]+a，其中0≤a＜1．

例如，3.2=[3.2]+0.2，5=[5]+0，－2.1=[－2.1]+0.9．

请你解决下列问题：

(1)、[4.8]= ， [－6.5]= ；

(2)、如果[x]=3，那么x的取值范围是；

(3)、如果[5x－2]=3x+1，那么x的值是；

(4)、如果x=[x]+a，其中0≤a＜1，且4a= [x]+1，求x的值．

查看试题解析