北京市石景山区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列几何体中,是圆柱的为( )A、
 B、
B、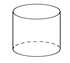 C、
C、 D、
D、 2. 2020年11月24日,长征五号遥五运载火箭在文昌航天发射场成功发射探月工程嫦娥五号探测器,火箭飞行2200秒后,顺利将探测器送入预定轨道,开启我国首次地外天体采样返回之旅.将 用科学记数法表示应为( )A、 B、 C、 D、3. 实数 在数轴上的对应点的位置如图所示,则正确的结论是( )
2. 2020年11月24日,长征五号遥五运载火箭在文昌航天发射场成功发射探月工程嫦娥五号探测器,火箭飞行2200秒后,顺利将探测器送入预定轨道,开启我国首次地外天体采样返回之旅.将 用科学记数法表示应为( )A、 B、 C、 D、3. 实数 在数轴上的对应点的位置如图所示,则正确的结论是( )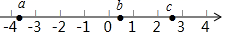 A、 B、 C、 D、4. 如图所示,点P到直线l的距离是( )
A、 B、 C、 D、4. 如图所示,点P到直线l的距离是( ) A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度5. 如果代数式 与 的值互为相反数,则 的值为( )A、 B、 C、 D、6. 如果 ,那么mn的值为( )A、-6 B、6 C、1 D、97. 某商场促销,把原价 元的空调以八折出售,仍可获利 元,则这款空调进价为( )A、 元 B、 元 C、 元 D、 元8. 对于两个不相等的有理数 , ,我们规定符号 表示 , 两数中较大的数,例如 .按照这个规定,那么方程 的解为( )A、-1 B、 C、1 D、-1或
A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度5. 如果代数式 与 的值互为相反数,则 的值为( )A、 B、 C、 D、6. 如果 ,那么mn的值为( )A、-6 B、6 C、1 D、97. 某商场促销,把原价 元的空调以八折出售,仍可获利 元,则这款空调进价为( )A、 元 B、 元 C、 元 D、 元8. 对于两个不相等的有理数 , ,我们规定符号 表示 , 两数中较大的数,例如 .按照这个规定,那么方程 的解为( )A、-1 B、 C、1 D、-1或二、填空题
-
9. 请写出一个比 大的负有理数: . (写出一个即可)10. 如图,点 在线段 上,若 , , 是线段 的中点,则 的长为 .
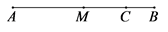 11. 计算: .12. 若 是关于 , 的二元一次方程组 的解,则 的值为 .13. 若 ,则 的值为 .14. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第七卷《盈不足》记载了一道有趣的数学问题:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?” 译文:“今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,总容量为2斛.问大容器、小容器的容量各是多少斛?”(注:斛,音hú,古量器名,亦是容量单位) 设大容器的容量为 斛,小容器的容量为 斛,根据题意,可列方程组为 .
11. 计算: .12. 若 是关于 , 的二元一次方程组 的解,则 的值为 .13. 若 ,则 的值为 .14. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第七卷《盈不足》记载了一道有趣的数学问题:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?” 译文:“今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,总容量为2斛.问大容器、小容器的容量各是多少斛?”(注:斛,音hú,古量器名,亦是容量单位) 设大容器的容量为 斛,小容器的容量为 斛,根据题意,可列方程组为 .
 15. 如图所示是一组有规律的图案,它们是由边长相同的小正方形组成,其中部分小正方形涂有阴影,按照这样的规律,第 个图案中有个涂有阴影的小正方形,第 个图案中有个涂有阴影的小正方形(用含有 的代数式表示).
15. 如图所示是一组有规律的图案,它们是由边长相同的小正方形组成,其中部分小正方形涂有阴影,按照这样的规律,第 个图案中有个涂有阴影的小正方形,第 个图案中有个涂有阴影的小正方形(用含有 的代数式表示).
三、解答题
-
16. 小石准备制作一个封闭的正方体盒子,他先用5个边长相等的正方形硬纸制作成如图所示的拼接图形(实线部分).请你在图中的拼接图形上再接上一个正方形,使得新拼接的图形经过折叠后能够成为一个封闭的正方体盒子(只需添加一个符合要求的正方形,并将添加的正方形用阴影表示).
 17. 写出计算结果:(1)、 ;(2)、 ;(3)、 ;(4)、 .18. 计算: .19. 计算: .20. 解方程: .21. 解方程:22. 解方程组:23. 先化简,再求值: ,其中 .24. 如图,点 , , 是同一平面内三个点,借助直尺、刻度尺、量角器完成(以答题卡上印刷的图形为准)
17. 写出计算结果:(1)、 ;(2)、 ;(3)、 ;(4)、 .18. 计算: .19. 计算: .20. 解方程: .21. 解方程:22. 解方程组:23. 先化简,再求值: ,其中 .24. 如图,点 , , 是同一平面内三个点,借助直尺、刻度尺、量角器完成(以答题卡上印刷的图形为准) (1)、画图:
(1)、画图:①连接 并延长到点 ,使得 ;
②画射线 ,画直线 ;
③过点 画直线 的垂线交 于点 .
(2)、测量:① 约为 (精确到 ;
②点 到直线 的距离约为 (精确到 .
25. 我国元代数学家朱世杰所撰写的《算学启蒙》中有这样一道题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”译文:良马平均每天能跑240里,驽马平均每天能跑150里.现驽马出发12天后良马从同一地点出发沿同一路线追它,问良马多少天能够追上驽马?
26. 已知: , , 平分 .求: 的度数.27. 关于 的一元一次方程 ,其中 是正整数 .(1)、当 时,求方程的解;(2)、若方程有正整数解 , 求 的值.28. 对于数轴上的点 ,线段 ,给出如下定义: 为线段 上任意一点,如果 , 两点间的距离有最小值,那么称这个最小值为点 ,线段 的“近距”,记作d1(点M,线段AB);如果 , 两点间的距离有最大值,那么称这个最大值为点 ,线段 的“远距”,记作d2(点M,线段AB).特别的,若点 与点 重合,则 , 两点间的距离为 .已知点 表示的数为 ,点 表示的数为 .例如图,若点 表示的数为 ,则d1(点C,线段AB)=2,d2(点C,线段AB)=7. (1)、若点 表示的数为 ,则d1(点D,线段AB)= , d2(点M,线段AB)= ;(2)、若点 表示的数为 ,点 表示的数为 .d2(点F,线段AB)是d1(点E,线段AB)的 倍.求 的值.
(1)、若点 表示的数为 ,则d1(点D,线段AB)= , d2(点M,线段AB)= ;(2)、若点 表示的数为 ,点 表示的数为 .d2(点F,线段AB)是d1(点E,线段AB)的 倍.求 的值.