北京市房山区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. $\frac{1}{4}$ 的相反数是（）

A、 $- \frac{1}{4}$ B、 $| - \frac{1}{4} |$ C、4 D、 $- 4$

查看试题解析
2. 从上面看几何体，则看到的是下面哪一个图形（）

A、 B、 C、 D、

查看试题解析
3. 随着京雄城际铁路全线贯通，雄安站同步投入运营，雄安站是京雄城际铁路的终点站，也是雄安新区第一个开工建设的大型基础设施工程，该站为桥式站，主体共5层，其中地上3层、地下2层，总建筑面积475000平方米．将475000用科学记数法表示为（）

A、 $4.75 \times 10^{4}$ B、 $4.75 \times 10^{5}$ C、 $47.5 \times 10^{4}$ D、 $47.5 \times 10^{5}$

查看试题解析
4. 下列四个图中，能用 $∠ 1$ 、 $∠ O$ 、 $∠ M O N$ 三种方法表示同一个角的是（）

A、 B、 C、 D、

查看试题解析
5. 有理数 $a$ ， $b$ 在数轴上的对应点的位置如图所示，则下列式子中正确的是（）

① $a < 0 < b$ ；② $| a | < | b |$ ；③ $a b > 0$ ；④ $a - b > a + b$

A、①② B、①④ C、②③ D、③④

查看试题解析
6. 如图，线段AB的长为m，点C为AB上一动点（不与A，B重合），D为AC中点，E为BC中点，随着点C的运动，线段DE的长度（）

A、随之变化 B、不改变，且为 $\frac{2}{3} m$ C、不改变，且为 $\frac{3}{5} m$ D、不改变，且为 $\frac{1}{2} m$

查看试题解析
7. 《算法统宗》是中国古代数学名著，作者是我国明代数学家程大位．在《算法统宗》中记载：“以绳测井，若将绳三折测之，绳多4尺，若将绳四折测之，绳多1尺，绳长井深各几何？”
译文：“用绳子测水井深度，如果将绳子折成三等份，井外余绳4尺；如果将绳子折成四等份，井外余绳1尺．问绳长、井深各是多少尺？”

设井深为x尺，根据题意列方程，正确的是（）

A、3（x+4）=4（x+1） B、3x+4=4x+1 C、3（x﹣4）=4（x﹣1） D、 $\frac{x}{3} - 4 = \frac{x}{4} - 1$

查看试题解析
8. 如图，白纸上放有一个表面涂满染料的小正方体．在不脱离白纸的情况下，转动正方体，使其各面染料都能印在白纸上，且各面仅能接触白纸一次，则在白纸上可以形成的图形为（）

A、①②③ B、①② C、①③ D、②④

查看试题解析

二、填空题

9. 小童买了3个练习本，5支签字笔，设练习本的单价为 $m$ 元，签字笔的单价为 $n$ 元，则小童共花费元．

查看试题解析
10. $- 3 a b^{2}$ 与是同类项．

查看试题解析
11. 计算： $46 ° 2 5^{'} + 53 ° 3 5^{'} =$ ．

查看试题解析
12. 已知 $| a - 2 | + {(b + 3)}^{2} = 0$ ，则 ${(a + b)}^{2021} =$ ．

查看试题解析
13. 关于 $x$ 的方程 $2 x + a = 1 - x$ 的解是 $x = - 2$ ，则 $a$ 的值为．

查看试题解析
14. 如图，点A、O、B在一条直线上，∠AOC=130°，OD是∠BOC的平分线，则∠COD=度．

查看试题解析
15. 数轴上点 $A$ 表示的数是2，点 $P$ 从点 $A$ 开始以每秒2个单位的速度在数轴上运动了3秒，这时点 $P$ 表示的数是

查看试题解析
16. 为了预防新型冠状病毒的传染，人员之间需要保持一米以上的安全距离．某公司会议室共有四行四列座椅，并且相邻两个座椅之间的距离超过一米，为了保证更加安全，公司规定在此会议室开会时，每一行、每一列均不能有连续三人就座．例如图1中第一列所示情况不满足条件（其中“√”表示就座人员）．根据该公司要求，该会议室最多可容纳的就座人数为人，并在图2中画出一种相应的座位安排示意图．

查看试题解析

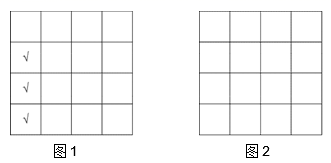
三、解答题

17. 计算： $10 - (- 5) + (- 9) + 6$ ．

查看试题解析
18. 计算： $- 3^{2} + (- 12) \times | - \frac{1}{2} | - 6 \div (- 1)$ .

查看试题解析
19. 解方程： $3 (2 x - 1) = 4 x + 3$ .

查看试题解析
20. 解方程： $\frac{5 x + 3}{4} = 1 - \frac{x - 1}{2}$ ．

查看试题解析
21. 先化简，再求值： $3 (3 x^{2} - x - 1) - (9 x^{2} - x + 3)$ ，其中 $x = - \frac{1}{3}$ ．

查看试题解析
22. 求代数式 $(5 a^{2} - a) - 2 (a^{2} - 2 a + 1)$ 的值，其中 $a^{2} + a + 3 = 0$

查看试题解析
23. 列方程解应用题：
霞云岭国家森林公园是集度假、休闲、养生于一体的旅游胜地．在放假期间，小方等同学与家长一起到公园游玩．下面是公园门票信息：

公园门票票价公示

成人票每张45元

学生票每张22元

小方爸爸说：咱们共11人，需要花费380元．请你算一算，他们中有多少成年人？多少学生？写出解答过程．

查看试题解析
24. 如图，平面上四个点 $A$ ， $B$ ， $C$ ， $D$ ．按要求完成下列问题：

(1)、①画线段 $A C$ ，连接 $B D$ ；
②画直线 $A B$ 与射线 $D C$ 相交于点 $E$ ；

(2)、用量角器度量 $∠ A E D$ 的大小为（精确到度）．

查看试题解析
25. 已知，如图，点 $M$ 、 $N$ 分别代表两个村庄，直线 $l$ 代表两个村庄之间的一条燃气管道，根据村民燃气需求，计划在管道 $l$ 上某处修建一座燃气管理站，向两村庄接入管道．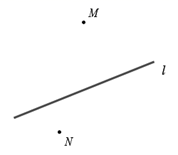

(1)、若计划建一个离村庄 $M$ 最近的燃气管理站，请画出燃气管理站的位置（用点 $P$ 表示），并写出这样做的依据．

(2)、若考虑到管道铺设费用问题，希望燃气管理站的位置到村庄 $M$ 、村庄 $N$ 距离之和最小，画出燃气管理站的位置（用点 $Q$ 表示），并写出这样做的依据．

查看试题解析
26. 补全解题过程．
如图所示，点 $C$ 是线段 $A B$ 的中点，延长线段 $A B$ 至点 $D$ ，使 $B D = \frac{1}{3} A B$ ，若 $B C = 3$ ，求线段 $C D$ 的长．

解：∵点 $C$ 是线段 $A B$ 的中点（已知）

∴ $A B =$ （）

∵ $B C = 3$ （已知）

∴ $A B =$ ．

∵延长线段 $A B$ 至点 $D$ ，使 $B D = \frac{1}{3} A B$ （已知）

∴ $B D =$ ．

∴ $C D =$ $+ B D =$ ．

查看试题解析
27. 已知： $∠ A O B = 60 °$ ，作射线 $O C$ ， $O D$ 为 $∠ A O C$ 平分线；将射线 $O D$ 绕点 $O$ 逆时针旋转 $90 °$ 得到射线 $O E$ ．设 $∠ C O D = α (0 ° < α < 90 °)$

(1)、如图1，射线 $O C$ 在 $∠ A O B$ 内部．当 $α = 10 °$ 时，求 $∠ E O B$ 的度数；

(2)、随着 $α$ 度数的变化，当 $∠ E O B = 2 ∠ B O C$ 时，求 $α$ 的值．

查看试题解析
28. 将 $n$ 个互不相同的整数置于一排，构成一个数组．在这 $n$ 个数字前任意添加“+”或“-”号，可以得到一个算式．若运算结果可以为0，我们就将这个数组称为“运算平衡”数组．

(1)、数组1，2，3，4是否是“运算平衡”数组？若是，请在以下数组中填上相应的符号，并完成运算；
1 2 3 4 =

(2)、若数组1，4，6， $m$ 是“运算平衡”数组，则 $m$ 的值可以是多少？

(3)、若某“运算平衡”数组中共含有 $n$ 个整数，则这 $n$ 个整数需要具备什么样的规律？

查看试题解析