黑龙江省哈尔滨市道里区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列各点中,在反比例函数 图象上的是( )A、(-1,8) B、(-2,4) C、(1,7) D、(2,4)2. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 袋子中装有4个黑球、2个白球,这些球的形状、大小、质地完全相同,即除颜色外无其他差别在看不到球的条件下,随机从袋中摸出1个球,是白球的概率是( )A、 B、 C、 D、4. 下面四个几何体中,主视图为三角形的是( )A、
3. 袋子中装有4个黑球、2个白球,这些球的形状、大小、质地完全相同,即除颜色外无其他差别在看不到球的条件下,随机从袋中摸出1个球,是白球的概率是( )A、 B、 C、 D、4. 下面四个几何体中,主视图为三角形的是( )A、 B、
B、 C、
C、 D、
D、 5. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、6. 如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
5. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、6. 如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( ) A、(1.5+150tanα) 米 B、(1.5+ )米 C、(1.5+150sinα)米 D、(1.5+ )米7. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( )
A、(1.5+150tanα) 米 B、(1.5+ )米 C、(1.5+150sinα)米 D、(1.5+ )米7. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( ) A、 B、 C、 D、8. 如图, 为 的外接圆,已知 为130°,则 的度数为( )
A、 B、 C、 D、8. 如图, 为 的外接圆,已知 为130°,则 的度数为( )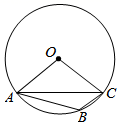 A、50° B、80° C、100° D、115°9. 如图,在 中,点D,E,F分别在AB,AC,BC上, , ,则下列式子一定正确的是( )
A、50° B、80° C、100° D、115°9. 如图,在 中,点D,E,F分别在AB,AC,BC上, , ,则下列式子一定正确的是( )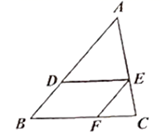 A、 B、 C、 D、10. 如图,抛物线 与x轴交于点 ,其对称轴为直线 ,结合图象给出下列结论:
A、 B、 C、 D、10. 如图,抛物线 与x轴交于点 ,其对称轴为直线 ,结合图象给出下列结论:① ;
② ;
③当 时,y随x的增大而增大;
④关于x的一元二次方程 有一个实数根.
其中正确的结论有( )
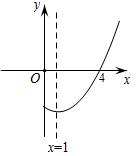 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
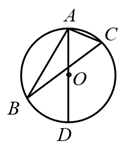
11. 在平面直角坐标系中,点 关于原点对称的点的坐标是 .12. 抛物线 的顶点坐标是 .13. 一辆汽车行驶的路程(单位:m)关于时间(单位:s)的函数解析式是 ,经过16s汽车行驶了m.14. 反比例函数 的图象经过点A( ,3),则 的值为 .15. 如图, 是 的外接圆 的直径,若 ,则 .
 16. 在 中, , , ,则AC的长为 .17. 若扇形的圆心角为45°,半径为6,则该扇形的弧长为 .18. AB 是 的弦, ,垂足为M,连接OA.若 中有一个角是30°, OM=3 ,则弦AB的长为 .19. 同时掷两枚质地均匀的骰子;两枚骰子点数之和为10的概率为 .20. 如图, 的中线AD与高CE交于点 , , , ,则AB的长为 .
16. 在 中, , , ,则AC的长为 .17. 若扇形的圆心角为45°,半径为6,则该扇形的弧长为 .18. AB 是 的弦, ,垂足为M,连接OA.若 中有一个角是30°, OM=3 ,则弦AB的长为 .19. 同时掷两枚质地均匀的骰子;两枚骰子点数之和为10的概率为 .20. 如图, 的中线AD与高CE交于点 , , , ,则AB的长为 .
三、解答题
-
21. 先化简,再求代数式 ,其中 .22. 如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A.B均在小正方形的顶点上.
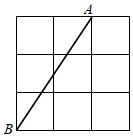 (1)、在图中画出等腰 ,点C在小正方形顶点上;(2)、在(1)的条件下确定点C后,再确定点D,点D在小正方形顶点上,请你连接DA,DC,DB,使 ,并求出四边形ADBC的面积.23. 为了解疫情期间学生网络学习的学习效果,高远中学随机抽取了部分学生进行调查.要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果.现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、在图中画出等腰 ,点C在小正方形顶点上;(2)、在(1)的条件下确定点C后,再确定点D,点D在小正方形顶点上,请你连接DA,DC,DB,使 ,并求出四边形ADBC的面积.23. 为了解疫情期间学生网络学习的学习效果,高远中学随机抽取了部分学生进行调查.要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果.现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题: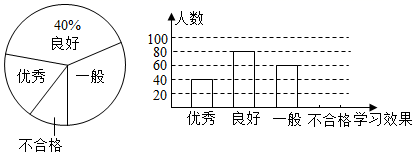 (1)、这次活动共抽查学生多少名?(2)、请通过计算补全条形统计图;(3)、若高远中学共有1600名学生,估计该中学“优秀”等次的学生有多少名?24. 如图,在 中, , ,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
(1)、这次活动共抽查学生多少名?(2)、请通过计算补全条形统计图;(3)、若高远中学共有1600名学生,估计该中学“优秀”等次的学生有多少名?24. 如图,在 中, , ,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.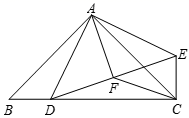 (1)、求证: ;(2)、在不添加任何辅助线的情况下,请直接写出图中所有的等腰直角三角形.25. 某班班主任对在某次考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,若购买甲种笔记本15个,乙种笔记本20个,共花费250元;若购买甲种笔记本10个,乙种笔记本25个,共花费225元.(1)、求购买一个甲种、一个乙种笔记本各需多少元?(2)、班主任决定再次购买甲、乙两种笔记本共35个,如果班主任此次购买甲、乙两种笔记本的总费用不超过300元,求至多需要购买多少个甲种笔记本?26. 内接于 , ,BD为 的直径, .
(1)、求证: ;(2)、在不添加任何辅助线的情况下,请直接写出图中所有的等腰直角三角形.25. 某班班主任对在某次考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,若购买甲种笔记本15个,乙种笔记本20个,共花费250元;若购买甲种笔记本10个,乙种笔记本25个,共花费225元.(1)、求购买一个甲种、一个乙种笔记本各需多少元?(2)、班主任决定再次购买甲、乙两种笔记本共35个,如果班主任此次购买甲、乙两种笔记本的总费用不超过300元,求至多需要购买多少个甲种笔记本?26. 内接于 , ,BD为 的直径, .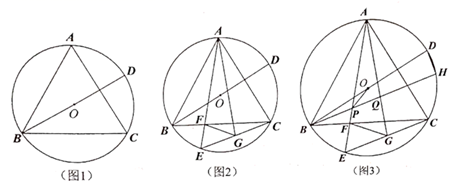 (1)、如图1,求证: 为等边三角形;(2)、如图2,弦AB交BC于点F,点G在EC上, ,求证: ;(3)、如图3,在(2)的条件下,弦BH分别交AF,AG于P,Q两点, , ,求QG的长.27. 在平面直角坐标系中,点 为坐标原点,抛物线 交 轴负半轴于点 ,交 轴正半轴于点 ,交 轴于点 , .
(1)、如图1,求证: 为等边三角形;(2)、如图2,弦AB交BC于点F,点G在EC上, ,求证: ;(3)、如图3,在(2)的条件下,弦BH分别交AF,AG于P,Q两点, , ,求QG的长.27. 在平面直角坐标系中,点 为坐标原点,抛物线 交 轴负半轴于点 ,交 轴正半轴于点 ,交 轴于点 , .
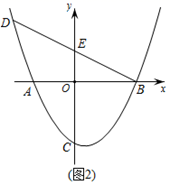
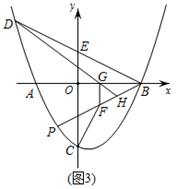 (1)、如图 ,求抛物线的解析式;(2)、如图 ,点 在抛物线上,且点 在第二象限,连接 交 轴于点 ,若 ,求点 的坐标;(3)、如图 ,在 的条件下,点 在抛物线上,且点 在第三象限,点 在 上, ,过点 作 轴的垂线,点 为垂足,连接 并延长交 于点 ,若 ,求 的长.
(1)、如图 ,求抛物线的解析式;(2)、如图 ,点 在抛物线上,且点 在第二象限,连接 交 轴于点 ,若 ,求点 的坐标;(3)、如图 ,在 的条件下,点 在抛物线上,且点 在第三象限,点 在 上, ,过点 作 轴的垂线,点 为垂足,连接 并延长交 于点 ,若 ,求 的长.