北京市通州区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
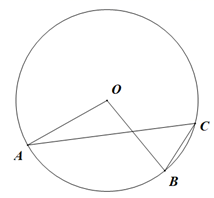
1. 抛物线 的顶点坐标是( )A、 B、 C、 D、2. 如图, 为⊙ 切线,连接 , .若 ,则 的度数为( )
 A、 B、 C、 D、3. 如图,在平面直角坐标系 中, 是反比例函数 图象上的一点,则 的面积为( )
A、 B、 C、 D、3. 如图,在平面直角坐标系 中, 是反比例函数 图象上的一点,则 的面积为( ) A、 B、 C、 D、4. 已知一个扇形的弧长为 ,半径是3,则这个扇形的面积为( )A、 B、 C、 D、5. 水平放置的圆柱形排水管道截面半径为1 m.若管道中积水最深处为0.4 m,则水面宽度为( )
A、 B、 C、 D、4. 已知一个扇形的弧长为 ,半径是3,则这个扇形的面积为( )A、 B、 C、 D、5. 水平放置的圆柱形排水管道截面半径为1 m.若管道中积水最深处为0.4 m,则水面宽度为( ) A、0.8 m B、1.2 m C、1.6 m D、1.8 m6. 古希腊人认为,最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”雕像便是如此.若某人身材大致满足黄金分割比例,且其肚脐至足底的长度为105 cm,则此人身高大约为( )
A、0.8 m B、1.2 m C、1.6 m D、1.8 m6. 古希腊人认为,最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”雕像便是如此.若某人身材大致满足黄金分割比例,且其肚脐至足底的长度为105 cm,则此人身高大约为( ) A、160 cm B、170 cm C、180 cm D、190 cm7. 已知抛物线的对称轴为 ,且经过点 , .则下列说法中正确的是( )A、若h=7,则a>0 B、若h=5,则a>0 C、若h=4,则a<0 D、若h=6,则a<08. 公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正 边形,使用刘徽割圆术,得到π的近似值为( )
A、160 cm B、170 cm C、180 cm D、190 cm7. 已知抛物线的对称轴为 ,且经过点 , .则下列说法中正确的是( )A、若h=7,则a>0 B、若h=5,则a>0 C、若h=4,则a<0 D、若h=6,则a<08. 公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正 边形,使用刘徽割圆术,得到π的近似值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. .10. 请写出一个开口向下且经过原点的抛物线解析式 .11. 如图, , , 为⊙ 上的点.若 ,则 .
 12. 如图,输电塔高 .在远离高压输电塔 的 处,小宇用测角仪测得塔顶的仰角为 .已知测角仪高 ,则 .
12. 如图,输电塔高 .在远离高压输电塔 的 处,小宇用测角仪测得塔顶的仰角为 .已知测角仪高 ,则 . 13. 如图,在 中, ,且DE分别交AB,AC于点D,E,若 ,则 与四边形 的面积之比等于 .
13. 如图,在 中, ,且DE分别交AB,AC于点D,E,若 ,则 与四边形 的面积之比等于 . 14. 如图,在平面直角坐标系 中,点 , , ,则点 坐标为 .
14. 如图,在平面直角坐标系 中,点 , , ,则点 坐标为 .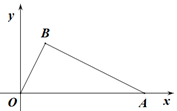 15. 在平面直角坐标系 中,点 为双曲线 上一点.将点 向左平移3个单位后,该点恰好出现在双曲线 上,则 的值为 .16. 如图,在平面直角坐标系 中,点 ,⊙ 的半径为3,点 为⊙ 上任意一点.则 的最大值为 .
15. 在平面直角坐标系 中,点 为双曲线 上一点.将点 向左平移3个单位后,该点恰好出现在双曲线 上,则 的值为 .16. 如图,在平面直角坐标系 中,点 ,⊙ 的半径为3,点 为⊙ 上任意一点.则 的最大值为 .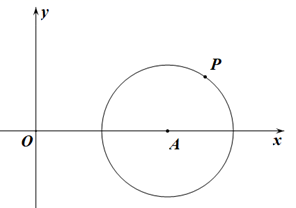
三、解答题
-
17. 如图, 与 交于 点, , , , ,求 的长.
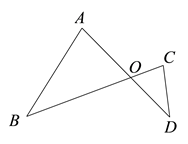 18. 二次函数 图象上部分点的横坐标x,纵坐标y的对应值如下表:
18. 二次函数 图象上部分点的横坐标x,纵坐标y的对应值如下表:x
…
…
…
y
…
…
…
(1)、该二次函数的对称轴为;(2)、求出二次函数的表达式.19. 下面是小付设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.
作法:如图,
①作射线OP;
②以点P为圆心,PO为半径作⊙P,与射线OP交于另一点B;
③分别以点O,点B为圆心,大于PO长为半径作弧,两弧交射线OP上方于点D;
④作直线PD;
则直线PD即为所求.
根据小付设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明:证明:∵ , ,
∴ ()(填推理的依据).
又∵ OP是⊙O的半径,
∴ PD是⊙O的切线()(填推理的依据).
20. 在平面直角坐标系 中,直线 与反比例函数 交于点 , . (1)、求出反比例函数表达式及 的值;(2)、根据函数图象,直接写出不等式 的解集.21. 如图,在 中, .以 为直径作⊙ ,交 于点 ,连接 .作 平分线,交 于点 ,交 于点 .
(1)、求出反比例函数表达式及 的值;(2)、根据函数图象,直接写出不等式 的解集.21. 如图,在 中, .以 为直径作⊙ ,交 于点 ,连接 .作 平分线,交 于点 ,交 于点 . (1)、求证: .(2)、若 , ,求 的长.22. 有这样一个问题:探究函数 的图象与性质.
(1)、求证: .(2)、若 , ,求 的长.22. 有这样一个问题:探究函数 的图象与性质.嘉瑶根据学习函数的经验,对函数 的图象与性质进行了探究.
下面是嘉瑶的探究过程,请补充完整:
(1)、函数 的图象与y轴交点;(填写“有”或“无”)(2)、下表是y与x的几组对应值:x
…
…
y
…
n
…
则n的值为;
(3)、如图,在平面直角坐标系xOy中,嘉瑶描出各对对应值为坐标的点.请你根据描出的点,帮助嘉瑶画出该函数的大致图象; (4)、请你根据探究二次函数与一元二次方程关系的经验,结合图象直接写出方程 的根约为 . (结果精确到0.1)23. 如图,将正方形 绕点 顺时针旋转 ,得到正方形 .连接 ,与正方形交于点 , ,连接 , .
(4)、请你根据探究二次函数与一元二次方程关系的经验,结合图象直接写出方程 的根约为 . (结果精确到0.1)23. 如图,将正方形 绕点 顺时针旋转 ,得到正方形 .连接 ,与正方形交于点 , ,连接 , . (1)、求 的值(用 表示);(2)、求证: ;(3)、写出线段 , , 之间的数量关系,并证明.24. 在平面直角坐标系 中,抛物线 与 轴交于点 , ,与 轴交于点 .
(1)、求 的值(用 表示);(2)、求证: ;(3)、写出线段 , , 之间的数量关系,并证明.24. 在平面直角坐标系 中,抛物线 与 轴交于点 , ,与 轴交于点 . (1)、求抛物线对称轴;(2)、求点 纵坐标(用含有 的代数式表示);(3)、已知点 .将点 向下移动一个单位,得到点 .若抛物线与线段 只有一个交点,求 的取值范围.25. 点 为平面直角坐标系 中一点,点 为图形 上一点.我们将线段 长度的最大值与最小值之间的差定义为点 视角下图形 的“宽度”.
(1)、求抛物线对称轴;(2)、求点 纵坐标(用含有 的代数式表示);(3)、已知点 .将点 向下移动一个单位,得到点 .若抛物线与线段 只有一个交点,求 的取值范围.25. 点 为平面直角坐标系 中一点,点 为图形 上一点.我们将线段 长度的最大值与最小值之间的差定义为点 视角下图形 的“宽度”. (1)、如图,⊙ 半径为2,与 轴, 轴分别交于点 , ,点 .
(1)、如图,⊙ 半径为2,与 轴, 轴分别交于点 , ,点 .①在点 视角下,⊙ 的“宽度”为 , 线段 的“宽度”为;
②点 为 轴上一点.若在点 视角下,线段 的“宽度”为 ,求 的取值范围:;
(2)、⊙ 的圆心在x轴上,半径为 ,直线 与x轴,y轴分别交于点 , .若线段 上存在点 ,使得在点 视角下,⊙ 的“宽度”可以为 ,求圆心 的横坐标 的取值范围.