北京市顺义区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 数轴上A、B、C、D四个点的位置如图所示，这四个点中，表示2的相反数的点是（）

A、点 A B、点B C、点C D、点D

查看试题解析
2. 如果 $5 a = 2 b$ （ $a b \neq 0$ ），那么下列比例式中正确的是（）

A、 $\frac{a}{b} = \frac{5}{2}$ B、 $\frac{b}{a} = \frac{2}{5}$ C、 $\frac{a}{2} = \frac{b}{5}$ D、 $\frac{a}{5} = \frac{b}{2}$

查看试题解析
3. 在Rt△ABC中， $∠ C = 90^{°}$ ， $A B = \sqrt{5}$ ， $A C = 2$ ，则tanB的值为（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
4. 将抛物线 $y = 2 x^{2}$ 向下平移1个单位，得到的抛物线是（）．

A、 $y = 2 x^{2} + 1$ B、 $y = 2 x^{2} - 1$ C、 $y = 2 {(x + 1)}^{2}$ D、 $y = 2 {(x - 1)}^{2}$

查看试题解析
5. 如图，在△ABC中，D、E分别是边AB、AC上的点，且DE∥BC，若AD：DB＝2：3，则△ADE与△ABC的面积比等于（）

A、2：3 B、4：5 C、4：9 D、4：25

查看试题解析
6. 二次函数的图象如图所示，则这个二次函数的表达式为（）

A、 $y = x^{2} + 2 x - 3$ B、 $y = x^{2} - 2 x - 3$ C、 $y = - x^{2} + 2 x - 3$ D、 $y = - x^{2} - 2 x + 3$

查看试题解析
7. 如图，点A，B，C都在⊙O上，若∠AOC=140°，则∠B的度数是（）

A、70° B、80° C、110° D、140°

查看试题解析

8. 已知抛物线

y = a x^{2} + b x + c

上部分点的横坐标x与纵坐标y的对应值如下表：

$x$	…	$- 4$	$- 3$	$- 2$	$- 1$	0	…
$y$	…	$- 3$	$m$	1	0	$- 3$	…

有以下几个结论：

①抛物线 $y = a x^{2} + b x + c$ 的开口向上；

②抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线 $x = - 2$ ；

③关于x的方程 $a x^{2} + b x + c = 0$ 的根为 $- 3$ 和 $- 1$ ；

④当y＜0时，x的取值范围是 $- 3$ ＜x＜ $- 1$ ．

其中正确的是（）

A、①④ B、②④ C、②③ D、③④

查看试题解析

二、填空题

9. 方程组 ${\begin{array}{l} x - y = 1 \\ 2 x + y = 5 \end{array}$ 的解是．

查看试题解析
10. 一个圆柱体容器内装入一些水，截面如图所示，若⊙O中的直径为52cm，水面宽AB＝48cm，则水的最大深度为cm．

查看试题解析
11. 小明为了测量一个小湖泊两岸的两棵树A、B之间的距离，在垂直AB的方向BC上确定点C，测得BC＝45m，∠C＝40°，从而计算出AB之间的距离．则AB＝．（精确到0.1m）（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）

查看试题解析
12. 如图，在⊙O中，若弧AB＝BC＝CD，则AC与2CD的大小关系是：AC2CD．（填“＞”，“＜”或“＝”）

查看试题解析
13. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，AB＝9，AC＝6，则cos∠DCB ＝．

查看试题解析
14. 如图，小明抛投一个沙包，沙包被抛出后距离地面的高度h（米）和飞行时间t（秒）近似满足函数关系式 $h = - \frac{1}{10} {(t - 6)}^{2} + 5$ ，则沙包在飞行过程中距离地面的最大高度是米．

查看试题解析
15. 在反比例函数 $y = \frac{k}{x}$ 的图象上有两点A（x₁ ， y₁），B（x₂ ， y₂），且x₁＜ x₂＜0，y₁＞ y₂写出一个符合条件的函数表达式．

查看试题解析
16. 如图，线段AB＝9，AC⊥AB于点A，BD⊥AB于点B，AC＝2，BD＝4，点P为线段AB上一动点，且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似，则AP的长为．

查看试题解析

三、解答题

17. 解不等式组： ${\begin{matrix} 3 (x + 1) > x - 1 \\ \frac{x + 9}{2} > 2 x \end{matrix}$ ．

查看试题解析
18. 计算： $| - \sqrt{3} | + {(π - 3)}^{0} - \sqrt{3} + 3 \tan 30^{°}$ ．

查看试题解析
19. 已知：如图，点M为锐角∠APB的边PA上一点．
求作：∠AMD，使得点D在边PB上，且∠AMD ＝2∠P．

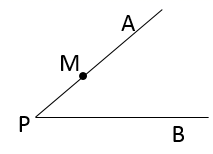
作法：①以点M为圆心，MP长为半径画圆，交PA于另一点C，交PB 于点D点；

②作射线MD．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：∵P、C、D都在⊙M上，

∠P为弧CD所对的圆周角，∠CMD为弧CD所对的圆心角，

∴∠P＝ $\frac{1}{2}$ ∠CMD（）（填推理依据）．

∴∠AMD ＝2∠P．

查看试题解析
20. 已知：如图，△ABC∽△ACD，CD平分∠ACB，AD ＝2，BD ＝3，求AC、DC的长．

查看试题解析
21. 一艘船向正北方向航行，在A处时看到灯塔S在船的北偏东30°的方向上，继续航行12海里到达B处，看到灯塔S在船的北偏东60°的方向上．若继续沿正北方向航行，求航行过程中船距灯塔S的最近距离．（结果精确到0.1海里）（参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
22. 已知： AB为⊙O的直径，点D为弧BC的中点，过点D作⊙O的切线交AB的延长线于点E，连接CB．

(1)、求证：BC∥DE；

(2)、若cosE＝ $\frac{4}{5}$ ， DE ＝20，求BC的长．

查看试题解析
23. 在平面直角坐标系xOy中，有抛物线 $y = x^{2} - 2 m x + m^{2}$ （ $m \geq 0$ ）．

(1)、求抛物线的顶点坐标（用含m的式子表示）；

(2)、过点A（0，1）作y轴的垂线l，点B在直线l上且横坐标是2m＋1
①若m的值等于1，求抛物线与线段AB的交点个数；

②若抛物线与线段AB只有一个公共点，直接写出m的取值范围．

查看试题解析
24. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D为线段BC上一动点（不与点B， C重合），作射线AD、AB，将射线AD、AB分别绕点A顺时针旋转90°，得到射线 $A D'$ ， $A B'$ ，过点B作BC的垂线，分别交射线 $A D'$ ， $A B'$ 于点E，F．

(1)、依题意补全图形；

(2)、求证：AB＝AF；

(3)、用等式表示线段AC，BD与BE之间的数量关系，并证明．

查看试题解析
25. 在平面直角坐标系xOy中，对于点P，若点Q满足条件：以线段PQ为对角线的正方形，边均与某条坐标轴垂直，则称点Q为点P的“正轨点”，该正方形为点P的“正轨正方形”如下图所示．

(1)、已知点A的坐标是（1，3）．
①在（－3，－1），（2，2），（3，3）中，是点A的“正轨点”的坐标是．

②若点A的“正轨正方形”的面积是4，写出一个点A的“正轨点”的坐标：

(2)、若点B（1，0）的“正轨点”在直线y＝2x＋2上，求点B的“正轨点”的坐标；

(3)、已知点C（m，0），若直线y＝2x＋m上存在点C的“正轨点”，使得点C的“正轨正方形”面积小于4，直接写出m的取值范围．

查看试题解析