北京市门头沟区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标是( )A、 B、 C、 D、2. 的半径为3,点 在 外,点 到圆心的距离为 ,则 需要满足的条件( )A、 B、 C、 D、无法确定3. 在 中, , , ,则 的长为( )
 A、2 B、3 C、 D、4. 点 ,点 ,在反比例函数 的图象上,且 ,则( )A、 B、 C、 D、不能确定5. 如图,在 中, , ,则 的度数是( )
A、2 B、3 C、 D、4. 点 ,点 ,在反比例函数 的图象上,且 ,则( )A、 B、 C、 D、不能确定5. 如图,在 中, , ,则 的度数是( ) A、10° B、20° C、30° D、40°6. 如果一个多边形的每一个外角都是60°,则这个多边形的边数是( )
A、10° B、20° C、30° D、40°6. 如果一个多边形的每一个外角都是60°,则这个多边形的边数是( )
A、3 B、4 C、5 D、67. 在大力发展现代化农业的形势下,现有 、 两种新玉米种子,为了了解它们的出芽情况,在推广前做了五次出芽实验,每次随机各自取相同种子数,在相同的培育环境中分别实验,实验情况记录如下:种子数量
100
300
500
1000
3000
出芽率
0.99
0.94
0.96
0.98
0.97
出芽率
0.99
0.95
0.94
0.97
0.96
下面有三个推断:
①当实验种子数量为100时,两种种子的出芽率均为0.99,所以 、 两种新玉米种子出芽的概率一样;
②随着实验种子数量的增加, 种子出芽率在0.97附近摆动,显示出一定的稳定性,可以估计A种子出芽的概率是0.97;
③在同样的地质环境下播种, 种子的出芽率可能会高于 种子.其中合理的是( )
A、①②③ B、①② C、①③ D、②③8. 如图,游乐园里的原子滑车是很多人喜欢的项目,惊险刺激,原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,原子滑车运行的竖直高度 (单位: )与水平距离 (单位: )近似满足函数关系 .下图记录了原子滑车在该路段运行的 与 的三组数据 、 、 ,根据上述函数模型和数据,可推断出,此原子滑车运行到最低点时,所对应的水平距离 满足( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图:在 中, , , ,则 .
 10. 如果一个二次函数图象开口向下,对称轴为 ,则该二次函数表达式可以为 . (任意写出一个符合条件的即可)11. 如图,在Rt△ABC中,∠C=90°,AB= 5,AC= 4,则cosA= .
10. 如果一个二次函数图象开口向下,对称轴为 ,则该二次函数表达式可以为 . (任意写出一个符合条件的即可)11. 如图,在Rt△ABC中,∠C=90°,AB= 5,AC= 4,则cosA= .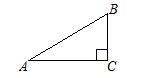 12. 如图,圆心角为120°,半径为4的弧,则这条弧的长度为是 .
12. 如图,圆心角为120°,半径为4的弧,则这条弧的长度为是 . 13. 如图所示的网格是正方形网格,则 °(点 , , , 是网格线交点)
13. 如图所示的网格是正方形网格,则 °(点 , , , 是网格线交点) 14. 已知正方形的边长为2cm,那么它外接圆的半径长是cm.15. 把抛物线y=2x2向上平移3个单位,得到的抛物线的解析式为.16. 如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为 ,三角形与正方形重叠部分的面积为 ,在下面的平面直角坐标系中,线段 表示的是三角形在正方形内部移动的面积图象, 点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 .
14. 已知正方形的边长为2cm,那么它外接圆的半径长是cm.15. 把抛物线y=2x2向上平移3个单位,得到的抛物线的解析式为.16. 如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为 ,三角形与正方形重叠部分的面积为 ,在下面的平面直角坐标系中,线段 表示的是三角形在正方形内部移动的面积图象, 点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 .

①
 ②
②  ③
③  17. 在数学课上,老师布置了一项作图任务,如下:已知:如图1,在 中, ,请在图中的 内(含边),画出使 的一个点 (保留作图痕迹),小红经过思考后,利用如下的步骤找到了点 :
17. 在数学课上,老师布置了一项作图任务,如下:已知:如图1,在 中, ,请在图中的 内(含边),画出使 的一个点 (保留作图痕迹),小红经过思考后,利用如下的步骤找到了点 :
①以 为直径,做 ,如图2;
②过点 作 的垂线,交 于点 ;
③以点 为圆心, 为半径作 ,分别交 、 边于 、 ,在劣弧上任取 一点 即为所求点,如图3.
问题:
(1)、在②的操作中,可以得到 °(依据:)(2)、在③的操作中,可以得到 °(依据:)三、解答题
-
18. 计算: .19. 已知二次函数 .
 (1)、用配方法将其化为 的形式;(2)、在所给的平面直角坐标系 中,画出它的图象.20. 如图,点 是反比例函数 的图象上的一点.
(1)、用配方法将其化为 的形式;(2)、在所给的平面直角坐标系 中,画出它的图象.20. 如图,点 是反比例函数 的图象上的一点. (1)、求该反比例函数的表达式;(2)、设直线 与双曲线 的两个交点分别为 和 ,当 时,直接写出 的取值范围.21. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小明同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点 处测得旗杆顶部 的仰角 为45°,旗杆底部 的俯角 为60°.室外测量组测得 的长度为5米,求旗杆 的高度.
(1)、求该反比例函数的表达式;(2)、设直线 与双曲线 的两个交点分别为 和 ,当 时,直接写出 的取值范围.21. 数学实践课上,同学们分组测量教学楼前国旗杆的高度.小明同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点 处测得旗杆顶部 的仰角 为45°,旗杆底部 的俯角 为60°.室外测量组测得 的长度为5米,求旗杆 的高度.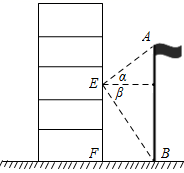 22. 如图,已知 是 的直径,点 在 的延长线上, , 切 于点 ,交 于点 ,连接 .
22. 如图,已知 是 的直径,点 在 的延长线上, , 切 于点 ,交 于点 ,连接 . (1)、求证: ;(2)、连结 ,如果 , ,求 的长.23. 已知:抛物线 经过点 和 .
(1)、求证: ;(2)、连结 ,如果 , ,求 的长.23. 已知:抛物线 经过点 和 . (1)、求抛物线的表达式;(2)、设 点关于对称轴的对称点为 ,抛物线 与线段 恰有一个公共点,结合函数图象,求 的取值范围.24. 在菱形 中, ,点 是对角线 上一点,连接 , ,将线段 绕点 逆时针旋转 并延长得到射线 ,交 的延长线于点 .(1)、依题意补全图形;
(1)、求抛物线的表达式;(2)、设 点关于对称轴的对称点为 ,抛物线 与线段 恰有一个公共点,结合函数图象,求 的取值范围.24. 在菱形 中, ,点 是对角线 上一点,连接 , ,将线段 绕点 逆时针旋转 并延长得到射线 ,交 的延长线于点 .(1)、依题意补全图形; (2)、求证: ;(3)、用等式表示线段 , , 之间的数量关系: .25. 在平面直角坐标系 中,对于任意三点 、 、 我们给出如下定义:三点中横坐标的最大值与最小值的差我们称为“横距”;三点中纵坐标的最大值与最小值的差我们称之为“纵距”;若三点的横距与纵距相等,我们称这三点为“等距点”.
(2)、求证: ;(3)、用等式表示线段 , , 之间的数量关系: .25. 在平面直角坐标系 中,对于任意三点 、 、 我们给出如下定义:三点中横坐标的最大值与最小值的差我们称为“横距”;三点中纵坐标的最大值与最小值的差我们称之为“纵距”;若三点的横距与纵距相等,我们称这三点为“等距点”.

已知:点 ,点 :
(1)、在点 , , 中,与点 、 为等距点的是;(2)、点 为 轴上一动点,若 、 , 三点为等距点, 的值为;(3)、已知点 ,有一半径为1,圆心为 的 ,若 上存在点 ,使得 , , 三点为等距点,直接写出 的取值的范围.