初中数学湘教版八年级下册2.7正方形 同步练习
试卷更新日期：2021-03-12 类型：同步测试
一、单选题
-
1. 正方形ABCD中，对角线AC、BD交于点O，则∠CBO等于（ ）A、30° B、45° C、60° D、75°2. 如图，在正方形 中， 是 上的一点，且 ，则 的度数是（ ）
A、 B、 C、 D、3. 如图，已知四边形ABCD是正方形，E是AB延长线上一点，且BE=BD，则∠BDE的度数是（ ）
A、22.5° B、30° C、45° D、67.5°4. 如图，四边形ABCD是正方形，直线L1、L2、L3 ， 若L1与L2的距离为5，L2与L3的距离7，则正方形ABCD的面积等于（ ）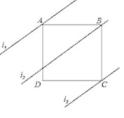
A、70 B、74 C、144 D、1485. 下列说法正确的个数是（ ）①对角线互相垂直或有一组邻边相等的矩形是正方形；②对角线相等或有一个角是直角的菱形是正方形；③对角线互相垂直且相等的平行四边形是正方形；④对角线互相垂直平分且相等的四边形是正方形.
A、1个 B、2个 C、3个 D、4个6. 如图，四边形ABCD中，AC、BD交于点O，则根据下列条件能判定它是正方形的是（ ）
A、∠DAB=90°且AD=BC B、AB=BC且AC=BD C、∠DAB=90°且AC⊥BD D、AC⊥BD且AO=BO=CO=DO7. 顺次连接四边形各边中点所构成的四边形是正方形，则原四边形可能是（ ）A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图，把一个长方形的纸片对折两次，然后剪下一个角，要得到一个正方形，剪口与折痕所成锐角的大小为（ ）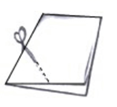
A、 B、 C、 D、9. 如图①、图②，在给定的一张矩形纸片上作一个正方形，甲、乙两人的作法如下：甲：以点A为圆心，AD长为半径画弧，交AB于点E，以点D为圆心，AD长为半径画弧，交CD于点F，连接EF，则四边形AEFD即为所求；
乙：作∠DAB的平分线，交CD于点M，同理作∠ADC的平分线，交AB于点N，连接MN，则四边形ADMN即为所求．
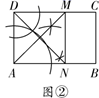
对于以上两种作法，可以做出的判定是（ ）
A、甲正确，乙不正确 B、甲、乙正确 C、乙正确，甲不正确 D、甲、乙均不正确10. 如图，点 、 分别是正方形 的边 、 上的点，且 ， 、 相交于点 ，下列结论：① ；② ；③ ，其中一定正确的有（ ）
A、0个 B、1个 C、2个 D、3个二、填空题
-
11. 若一个正方形的面积为a2+a+ ，则此正方形的周长为.12. 如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形的边长为
13. 如图，E为正方形ABCD对角线BD上一点，且BE=BC，则∠DCE= ．
14. 在平行四边形ABCD中，对角线AC，DB相交于点O.要使四边形ABCD是正方形，还需添加一组条件．下面给出了四组条件：①AB⊥AD，且AB＝AD；②AB＝BD，且AB⊥BD；③OB＝OC，且OB⊥OC；④AB＝AD，且AC＝BD.其中正确的是.(填序号)15. 如图，已知P是正方形ABCD对角线BD上一点，且BP=BC，则 的值为 ．
三、解答题
-
16.
如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线AC于点G，且DE=DG；
（1）求证：AE=CG；
（2）求证：BE∥DF．
17.如图，△ABC是等腰直角三角形，∠A=90°，点P、Q分别是AB、AC上的一动点，且满足BP=AQ，D是BC的中点．
（1）求证：△PDQ是等腰直角三角形；
（2）当点P运动到什么位置时，四边形APDQ是正方形，并说明理由．
四、综合题
