北京市丰台区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 函数y=(x+1)²-2的最小值是（）

A、1　　 B、－1　 C、2　 D、－2

查看试题解析
2. 下面是利用图形变化的知识设计的一些美丽的图案，其中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若一个扇形的圆心角为90°，半径为6，则该扇形的面积为（）

A、 $\frac{3 π}{2}$ B、 $3 π$ C、 $6 π$ D、 $9 π$

查看试题解析
4. 点 $A (- 1 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (2 ， y_{3})$ 是反比例函数 $y = \frac{2}{x}$ 图象上的三个点，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{2} < y_{1}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
5. 直径为10分米的圆柱形排水管，截面如图所示．若管内有积水（阴影部分），水面宽AB为8分米，则积水的最大深度CD为（）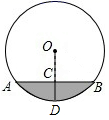

A、2分米 B、3分米 C、4分米 D、5分米

查看试题解析

6. 二次函数

y = a x^{2} + b x + c

（

a \neq 0

）的图象是抛物线G，自变量x与函数y的部分对应值如下表：

x	…	﹣5	﹣4	﹣3	﹣2	﹣1	0	…
y	…	4	0	﹣2	﹣2	0	4	…

下列说法正确的是（）

A、抛物线G的开口向下 B、抛物线G的对称轴是直线

x = - 2

C、抛物线G与y轴的交点坐标为（0，4） D、当x＞﹣3时，y随x的增大而增大

查看试题解析

7. 如图，点O为线段AB的中点，点B，C，D到点O的距离相等，连接AC，BD．则下面结论不一定成立的是（）

A、∠ACB=90° B、∠BDC=∠BAC C、AC平分∠BAD D、∠BCD+∠BAD=180°

查看试题解析
8. 函数 $y = \frac{1}{2} + \frac{1}{x^{2}}$ 的图象如图所示，若点 $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ 是该函数图象上的任意两点，下列结论中错误的是（）

A、 $x_{1} \neq 0$ ， $x_{2} \neq 0$ B、 $y_{1} > \frac{1}{2}$ ， $y_{2} > \frac{1}{2}$ C、若 $y_{1} = y_{2}$ ，则 $| x_{1} | = | x_{2} |$ D、若 $y_{1} < y_{2}$ ，则 $x_{1} < x_{2}$

查看试题解析

二、填空题

9. 将抛物线y=x²向下平移2个单位长度，平移后拋物线的解析式为．

查看试题解析
10. 如图，在平行四边形ABCD中，点 $E$ 在边 $A D$ 上， $A C ， B E$ 交于点 $O$ ，若 $A E ： E D = 1 ： 2$ ，则 $S_{△ A O E} ： S_{△ C O B}$ = ．

查看试题解析

11. 林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组统计数据：

移植的棵数n	1000	1500	2500	4000	8000	15000	20000	30000
成活的棵数m	865	1356	2220	3500	7056	13170	17580	26430
成活的频率 $\frac{m}{n}$	0.865	0.904	0.888	0.875	0.882	0.878	0.879	0.881

估计该种幼树在此条件下移植成活的概率为．（精确到0.01）

查看试题解析

12. 抛物线 $y = x^{2} + b x + 4$ 与x轴有且只有1个公共点，则b= ．

查看试题解析
13. 如图， $⊙ O$ 是 $Δ A B C$ 的外接圆，D是 $\overset{⌢}{A C}$ 的中点，连结 $A D ， B D$ ，其中 $B D$ 与 $A C$ 交于点E. 写出图中所有与 $Δ A D E$ 相似的三角形：.

查看试题解析
14. 如图，为了测量操场上一棵大树的高度，小英拿来一面镜子，平放在离树根部5m的地面上，然后她沿着树根和镜子所在的直线后退，当她后退1m时，正好在镜中看见树的顶端．小英估计自己的眼睛到地面的距离为1.6m，则大树的高度是m．

查看试题解析
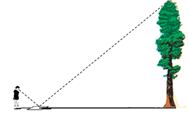15. 如图， $△$ ABC是⊙O的内接三角形，OD⊥BC于点D．下面是借助直尺，画出 $△$ ABC中∠BAC的平分线的步骤：
①延长OD交 $\overset{⌢}{B C}$ 于点M；

②连接AM交BC于点N．

所以∠BAN=∠CAN．

即线段AN为所求 $△$ ABC中∠BAC的平分线．

请回答，得到∠BAN=∠CAN的依据是．

查看试题解析
16. 2020年3月14日是全球首个国际圆周率日（π Day）．历史上求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔 $\cdot$ 卡西的计算方法是：当正整数n充分大时，计算某个圆的内接正6n边形的周长和外切正6n边形 $($ 各边均与圆相切的正6n边形 $)$ 的周长，再将它们的平均数作为2π的近似值．当n=1时，右图是⊙O及它的内接正六边形和外切正六边形．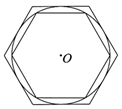

(1)、若⊙O的半径为1，则⊙O的内接正六边形的边长是；

(2)、按照阿尔 $\cdot$ 卡西的方法，计算n=1时π的近似值是．（结果保留两位小数）（参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析

三、解答题

17. 已知二次函数 $y = x^{2} - 4 x + 3$ ．

(1)、求二次函数 $y = x^{2} - 4 x + 3$ 图象的顶点坐标；

(2)、在平面直角坐标系xOy中，画出二次函数 $y = x^{2} - 4 x + 3$ 的图象；

(3)、当 $1 < x < 4$ 时，结合函数图象，直接写出y的取值范围．

查看试题解析
18. 如图，在 $△ A B C$ 中，点D，E分别在边AB，AC上，连接DE，且 $A D \cdot A B = A E \cdot A C$ ．

(1)、求证： $△$ ADE∽ $△$ ACB；

(2)、若∠B=55°，∠ADE =75°，求∠A的度数．

查看试题解析
19. 如图，在平面直角坐标系xOy中，△AOB的顶点坐标分别是A（1，0），O（0，0），B（2，2）．

(1)、画出 $△$ A₁OB₁ ，使 $△$ A₁OB₁与 $△$ AOB关于点O中心对称；

(2)、以点O为位似中心，将 $△$ AOB放大为原来的2倍，得到 $△$ A₂OB₂ ，画出一个满足条件的 $△$ A₂OB₂ ．

查看试题解析
20. 如图，在平面直角坐标系xOy中，A（4，0），C（0，2）．点D是矩形OABC对角线的交点．已知反比例函数 $y = \frac{k}{x}$ （ $k \neq 0$ ）在第一象限的图象经过点D，交BC于点M，交AB于点N．

(1)、求点D的坐标和k的值；

(2)、反比例函数图象在点M到点N之间的部分（包含M， N两点）记为图形G，求图形G上点的横坐标x的取值范围．

查看试题解析
21. 如图， AC与⊙O相切于点C， AB经过⊙O上的点D，BC交⊙O于点E，DE∥OA，CE是⊙O的直径．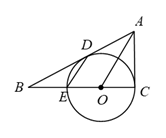

(1)、求证：AB是⊙O的切线；

(2)、若BD＝4，CE＝6，求AC的长．

查看试题解析
22. 在倡议“绿色环保，公交出行”的活动中，学生小志对公交车的计价方式进行了研究．他发现北京公交集团的公交车站牌中都写有：“10公里以内（含）票价2元，每增加5公里以内（含）加价1元”，如下图．

小志查阅了相关资料，了解到北京公交车的票价按照乘客乘坐公交车的里程（公里）数计算，乘客可以按照如下方法计算票价：

①站牌中每一站上面标注的数字表示该站的站位号，乘客可以通过计算上、下车站的站位号的差，得到乘车的大致里程数，然后按照下面具体标准得出票价：若里程数在0至10之间（含0和10，下同），则票价为2元；若里程数在11至15之间，则票价为3元；若里程数在16至20之间，则票价为4元，以此类推．

②为了鼓励市民绿色出行，北京公交集团制定了票价优惠政策：使用市政公交一卡通刷卡，普通卡打5折，学生卡打2.5折．

请根据上述信息，回答下列问题：

(1)、学生甲想去抗战雕塑园参观，他乘坐339路公交车从云岗站上车，到抗战雕塑园站下车，那么原票价应为元，他使用学生卡实际支付元；

(2)、学生乙使用学生卡乘339路公交车去北京西站，若下车刷卡时实际支付了1元，则他在佃起村上车的概率为．

查看试题解析
23. 在平面直角坐标系xOy中，抛物线 $y = a x^{2} + b x$ （ $a \neq 0$ ）过点（4，0）．

(1)、用含a的代数式表示b；

(2)、已知点A（0，a），将点A绕原点O顺时针旋转90°得到点B，再将点B向右平移2个单位长度得到点C，求点C的坐标（用含a的代数式表示）；

(3)、在（2）的条件下，若线段AC与抛物线有公共点，求a的取值范围．

查看试题解析
24. 如图1，正方形ABCD中，点E是BC延长线上一点，连接DE，过点B作BF⊥DE于点F，连接FC
．

(1)、求证：∠FBC=∠CDF．

(2)、作点C关于直线DE的对称点G，连接CG，FG．
①依据题意补全图形；

②用等式表示线段DF，BF，CG之间的数量关系并加以证明．

查看试题解析
25. 对于平面直角坐标系xOy中的点P和图形M，给出如下定义：若在图形M上存在点Q，使得OQ=kOP，k为正数，则称点P为图形M的k倍等距点．已知点A（－2，2），B（2，2）．

(1)、在点C（1，0），D（0，-2），E（1，1）中，线段AB的2倍等距点是；

(2)、画出线段AB的所有2倍等距点形成的图形（用阴影表示），并求该图形的面积；

(3)、已知直线y=－x+b与x轴，y轴的交点分别为点F， G，若线段FG上存在线段AB的2倍等距点，直接写出b的取值范围．

查看试题解析