北京市房山区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. sin30°的值等于( )A、 B、 C、 D、13. 如图,在 中, ∥ ,若 , ,则 等于( )
2. sin30°的值等于( )A、 B、 C、 D、13. 如图,在 中, ∥ ,若 , ,则 等于( ) A、 B、 C、 D、4. 如图, , 是⊙ 的半径,若 ,则 的度数是( )
A、 B、 C、 D、4. 如图, , 是⊙ 的半径,若 ,则 的度数是( )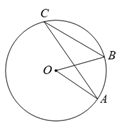 A、 B、 C、 D、5. 在半径为 的圆中, 的圆心角所对的弧长为( )A、 B、 C、 D、6. 若点 , , 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、7. 在 中, , , ,则 的长为( )A、 B、2 C、 或4 D、2或48. 如图,二次函数 的图象经过 , , 三点,下面四个结论中正确的是( )
A、 B、 C、 D、5. 在半径为 的圆中, 的圆心角所对的弧长为( )A、 B、 C、 D、6. 若点 , , 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、7. 在 中, , , ,则 的长为( )A、 B、2 C、 或4 D、2或48. 如图,二次函数 的图象经过 , , 三点,下面四个结论中正确的是( ) A、抛物线开口向下 B、当 时, 取最小值 C、当 时,一元二次方程 必有两个不相等实根 D、直线 经过点 , ,当 时, 的取值范围是
A、抛物线开口向下 B、当 时, 取最小值 C、当 时,一元二次方程 必有两个不相等实根 D、直线 经过点 , ,当 时, 的取值范围是二、填空题
-
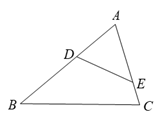
9. 已知 ,则 .10. 请写出一个过点 的函数表达式: .11. 已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是.12. 函数 的图象向下平移3个单位,得到函数图象的表达式是 .13. 如图,点 , 分别在△ 的 , 边上.只需添加一个条件即可证明△ ∽△ ,这个条件可以是 . (写出一个即可)
 14. 如图,AB为 的直径,弦 于点H , 若 , ,则OH的长度为 .
14. 如图,AB为 的直径,弦 于点H , 若 , ,则OH的长度为 .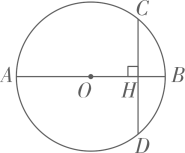 15. 如图所示的网格是边长为1的正方形网格, , , 是网格线交点,则 .
15. 如图所示的网格是边长为1的正方形网格, , , 是网格线交点,则 .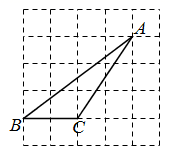 16. 我们将满足等式 的每组 , 的值在平面直角坐标系中画出,便会得到如图所示的“心形”图形.下面四个结论中:
16. 我们将满足等式 的每组 , 的值在平面直角坐标系中画出,便会得到如图所示的“心形”图形.下面四个结论中:①“心形”图形是轴对称图形;
②“心形”图形所围成的面积小于3;
③“心形”图形上任意一点到原点的距离都不超过 ;
④“心形”图形恰好经过6个整点(即横、纵坐标均为整数的点).
所有正确结论的序号是 .

三、解答题
-
17. 如图,已知 ∥ , .求证: .
 18. 已知二次函数 .
18. 已知二次函数 . (1)、求它的图象的顶点坐标和对称轴;(2)、画出它的图象,并结合图象,当 时,求 的取值范围.19. 已知:线段 .
(1)、求它的图象的顶点坐标和对称轴;(2)、画出它的图象,并结合图象,当 时,求 的取值范围.19. 已知:线段 .
求作: ,使其斜边 ,一条直角边 .
作法:①作线段 ;
②分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 交 于点 ;
③以 为圆心, 长为半径作⊙ ;
④以点 为圆心,线段 的长为半径作弧交⊙ 于点 ,连接 . 就是所求作的直角三角形.
 (1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵点 在线段 的垂直平分线上,
∴点 为线段 的中点, 为⊙ 的半径.
∴ 为⊙ 的直径.
∵点 在⊙ 上,
∴ ()(填推理的依据).
∴ 为直角三角形.
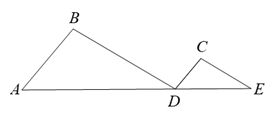
20. 在“综合与实践”活动中,某校九年级数学小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 的上方 的点 处悬停,此时测得桥两端 , 两点的俯角分别为 和 ,求桥 的长度.(结果精确到 .参考数据: , ) 21. 如图,一次函数 的图象与 轴交于点 ,与反比例函数 的图象交于点 .
21. 如图,一次函数 的图象与 轴交于点 ,与反比例函数 的图象交于点 . (1)、求 的值;(2)、点 为 轴上一动点.若 的面积是 ,请直接写出点 的坐标.22. 如图, 为⊙ 的直径,⊙ 过 的中点 , ,垂足为点 .
(1)、求 的值;(2)、点 为 轴上一动点.若 的面积是 ,请直接写出点 的坐标.22. 如图, 为⊙ 的直径,⊙ 过 的中点 , ,垂足为点 .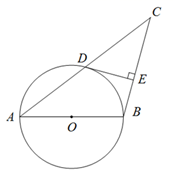 (1)、求证: 与⊙ 相切;(2)、若 , .求 的长.23. 已知抛物线 经过点 .(1)、当抛物线与 轴交于点 时,求抛物线的表达式;(2)、设抛物线与 轴两交点之间的距离为 .当 时,求 的取值范围.24. 如图,已知 是矩形 的一条对角线,点 在 的延长线上,且 .连接 ,与 相交于点 ,与 相交于点 .
(1)、求证: 与⊙ 相切;(2)、若 , .求 的长.23. 已知抛物线 经过点 .(1)、当抛物线与 轴交于点 时,求抛物线的表达式;(2)、设抛物线与 轴两交点之间的距离为 .当 时,求 的取值范围.24. 如图,已知 是矩形 的一条对角线,点 在 的延长线上,且 .连接 ,与 相交于点 ,与 相交于点 . (1)、依题意补全图形;(2)、若 ,解答下列问题:
(1)、依题意补全图形;(2)、若 ,解答下列问题:①判断 与 的位置关系,并说明理由;
②连接 ,用等式表示线段 , , 之间的数量关系,并证明.
25. 定义:在平面直角坐标系 中,点 为图形 上一点,点 为图形 上一点.若存在 ,则称图形 与图形 关于原点 “平衡”.(1)、如图,已知⊙ 是以 为圆心, 为半径的圆,点 , , .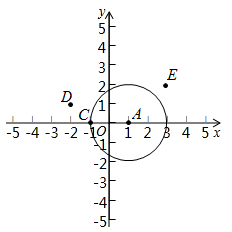
①在点 , , 中,与⊙ 关于原点 “平衡”的点是;
②点 为直线 上一点,若点 与⊙ 关于原点 “平衡”,点 的横坐标的取值范围为:;
(2)、如图,已知图形 是以原点 为中心,边长为 的正方形.⊙ 的圆心在 轴上,半径为 .若⊙ 与图形 关于原点 “平衡”,请直接写出圆心 的横坐标的取值范围.