安徽省六安市2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，绕某个点旋转72度后能与自身重合的是（　　）

A、 B、 C、 D、

查看试题解析
2. 若关于x的一元二次方程的两个根为x₁=1，x₂=2，则这个方程可能是（）

A、x²-3x+2=0 B、x²+3x+2=0 C、x²+3x-2=0 D、x²-2x+3=0

查看试题解析
3. 下列事件是必然事件的是( )

A、某运动员射击一次击中靶心 B、抛一枚硬币，正面朝上 C、3个人分成两组，一定有2个人分在一组 D、明天一定是晴天

查看试题解析
4. 把抛物线y=﹣x²向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（）

A、y=﹣（x﹣1）²﹣3 B、y=﹣（x+1）²﹣3 C、y=﹣（x﹣1）²+3 D、y=﹣（x+1）²+3

查看试题解析
5. 若 $y = (2 - m) x^{m^{2} - 3}$ 是二次函数，且开口向上，则m的值为（）

A、 $\pm \sqrt{5}$ B、 $\sqrt{5}$ C、 $- \sqrt{5}$ D、0

查看试题解析
6. 现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为 $x$ 、小明掷B立方体朝上的数字为 $y$ 来确定点P（ $x ， y$ ），那么他们各掷一次所确定的点P落在已知抛物线 $y = - x^{2} + 4 x$ 上的概率为（）

A、 $\frac{1}{18}$ B、 $\frac{1}{12}$ C、 $\frac{1}{9}$ D、 $\frac{1}{6}$

查看试题解析
7. 已知一个圆锥的底面半径为3cm，母线长为10cm，则这个圆锥的侧面积为（　　）

A、15πcm² B、30πcm² C、60πcm² D、3 $\sqrt{91}$ cm²

查看试题解析
8.
如图，在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y=x的图象被⊙P截得的弦AB的长为 $2 \sqrt{3}$ ，则a的值是（）

A、2 $\sqrt{2}$ B、2+ $\sqrt{2}$ C、2 $\sqrt{3}$ D、2+ $\sqrt{3}$

查看试题解析
9. 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB＝30°，CD＝2 $\sqrt{3}$ ，则阴影部分图形的面积为（）

A、4π B、2π C、π D、 $\frac{2 π}{3}$

查看试题解析
10. 二次函数y=ax²+bx+c图象如图，下列正确的个数为（）
①bc＞0；

②2a﹣3c＜0；

③2a+b＞0；

④ax²+bx+c=0有两个解x₁ ， x₂ ， x₁＞0，x₂＜0；

⑤a+b+c＞0；

⑥当x＞1时，y随x增大而减小．

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 已知关于x的二次方程（1﹣2k）x²﹣2x﹣1=0有实数根，则k的取值范围是．

查看试题解析
12. 如图，等边△ADE由△ABC绕点A逆时针旋转40°得到，其中AD与BC相交于点F，则∠AFB= ．

查看试题解析
13. 如图，在Rt $△$ AOB中，OA=OB=3 ，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为．

查看试题解析
14.
二次函数 $y = \sqrt{3} x^{2}$ 的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数 $y = \sqrt{3} x^{2}$ 的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积为 .

查看试题解析

三、解答题

15. 解方程

(1)、x²–9 = 0

(2)、x²+4x -1= 0

查看试题解析
16. 已知关于x的方程x²－（2k－1）x+k²=0有两个实数根x₁ ， x₂ ．

(1)、求k的取值范围；

(2)、若∣x₁+x₂∣= x₁x₂-1，求k的值．

查看试题解析
17. 已知二次函数y=﹣x²+x+4．

(1)、求抛物线的顶点坐标和对称轴；

(2)、当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减小？当x取何值时，y有最大值还是最小值？是多少？

查看试题解析
18. 如图，在△ABC中，∠ACB=90°，E为BC上一点，以CE为直径作⊙O，AB与⊙O相切于点D，连接CD，若BE=OE=2．

(1)、求证：∠A=2∠DCB；

(2)、求图中阴影部分的面积（结果保留π和根号）．

查看试题解析
19. 如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．

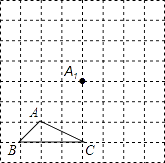
（1）把△ABC沿BA方向平移后，点A移到点A₁ ，在网格中画出平移后得到的△A₁B₁C₁；
（2）把△A₁B₁C₁绕点A₁按逆时针方向旋转90°，在网格中画出旋转后的△A₁B₂C₂；
（3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．

查看试题解析
20. 小明和小亮玩一个游戏：三张大小、质地都相同的卡片上分别标有数字3、4、5，现将标有数字的一面朝下．小明从中任意抽取一张，记下数字后放回洗匀，然后小亮从中任意抽取一张，计算小明和小亮抽得的两个数字之和．如果和为奇数，则小明胜；和为偶数，则小亮胜．

(1)、请你用画树状图或列表的方法，求出这两数和为8的概率；

(2)、你认为这个游戏对双方公平吗？说说你的理由．

查看试题解析
21. 列方程（组）解应用题：
据媒体报道，2011年某市市民到郊区旅游总人数约500万人，2013年到郊区旅游总

人数增长到约720万人．

(1)、求这两年该市市民到郊区旅游总人数的年平均增长率．

(2)、若该市到郊区旅游的总人数年平均增长率不变，请你预计2014年有多少市民到郊区旅游．

查看试题解析
22. 某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数： $y = - 10 x + 500$ ．

(1)、设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？

(2)、如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？

(3)、根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？
（成本＝进价×销售量）

查看试题解析
23. 如图，直线y= $\frac{\sqrt{3}}{3}$ x+ $\sqrt{3}$ 与x轴交于点A，与y轴交于点C，以AC为直径作⊙M，点D是劣弧AO上一动点（D点与A，C不重合）．抛物线y=－ $\frac{\sqrt{3}}{3}$ x²+bx+c经过点A、C，与x轴交于另一点B，

(1)、求抛物线的解析式及点B的坐标；

(2)、在抛物线的对称轴上是否存在一点P，是︱PA—PC︱的值最大；若存在，求出点P的坐标；若不存在，请说明理由．

(3)、连CD交AO于点F，延长CD至G，使FG=2，试探究当点D运动到何处时，直线GA与⊙M相切，并请说明理由．

查看试题解析