安徽省淮北市五校联考2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 如果 ,那么 的值是( )A、 B、 C、 D、2. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、3. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若反比例函数 的图像在第一、第三象限,则 可能取的一个值为( )A、0 B、1 C、2 D、35. 抛物线y=x2﹣9的顶点坐标是( )A、(0,﹣9) B、(﹣3,0) C、(﹣9,0) D、(3,0)6. 如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB的水平宽度AC为12米,则斜坡AB的长为( )
4. 若反比例函数 的图像在第一、第三象限,则 可能取的一个值为( )A、0 B、1 C、2 D、35. 抛物线y=x2﹣9的顶点坐标是( )A、(0,﹣9) B、(﹣3,0) C、(﹣9,0) D、(3,0)6. 如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB的水平宽度AC为12米,则斜坡AB的长为( ) A、4 米 B、6 米 C、6 米 D、24米7. 如图,在△ABC中,AC=3,BC=6,D为BC边上的一点,且∠BAC=∠ADC . 若△ADC的面积为a , 则△ABC的面积为( )
A、4 米 B、6 米 C、6 米 D、24米7. 如图,在△ABC中,AC=3,BC=6,D为BC边上的一点,且∠BAC=∠ADC . 若△ADC的面积为a , 则△ABC的面积为( )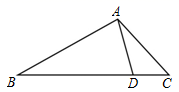 A、6a B、4a C、 D、8. 如图,在 中,O是 边上的点,以点O为圆心, 为半径的 与 相切于点 是优弧 上一点, ,则 的度数是( )
A、6a B、4a C、 D、8. 如图,在 中,O是 边上的点,以点O为圆心, 为半径的 与 相切于点 是优弧 上一点, ,则 的度数是( ) A、 B、 C、 D、9. 如图,一块含有 的直角三角板的直角顶点和坐标原点 重合, 角的顶点 在反比例函数 的图象上,顶点 在反比例函数 的图象上,则 的值为( )
A、 B、 C、 D、9. 如图,一块含有 的直角三角板的直角顶点和坐标原点 重合, 角的顶点 在反比例函数 的图象上,顶点 在反比例函数 的图象上,则 的值为( ) A、 B、8 C、 D、1210. 如图,A(12,0),B(0,9)分别是平面直解坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交于点P、Q,则线段PQ长度的最小值是( )
A、 B、8 C、 D、1210. 如图,A(12,0),B(0,9)分别是平面直解坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交于点P、Q,则线段PQ长度的最小值是( )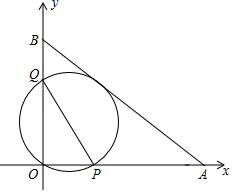 A、 B、10 C、7.2 D、
A、 B、10 C、7.2 D、二、填空题
-
11. 已知2是 和4的比例中项,则 .12. 图①中特种自行车的轮子形状为“勒络三角形”,图②是其一个轮子的示意图,“勒络三角形”是分别以等边三角形 三个顶点 为圆心,以边长为半径的三段弧围成的图形、若这个等边三角形 的边长为 则这种自行车一个轮子的周长为 .
 13. 如图,点 是反比例函数 图像上一点,过点 作 轴于点 ,点 , 在 轴上,且 ,四边形 的面积为4,则k= .
13. 如图,点 是反比例函数 图像上一点,过点 作 轴于点 ,点 , 在 轴上,且 ,四边形 的面积为4,则k= . 14. 如图, ,直角三角形 斜边的端点 , 分别在射线 , 上滑动, , ,连接 .当 平分 时, 的长为 .
14. 如图, ,直角三角形 斜边的端点 , 分别在射线 , 上滑动, , ,连接 .当 平分 时, 的长为 .
三、解答题
-
15. 计算: .16. 二次函数图象的顶点坐标是(-2,3),并经过点(1,2),求这个二次函数的函数关系式.17. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,3).
 (1)、画出△ABC绕点B逆时针旋转90°得到的△A1BC1 .(2)、以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△ABC放大后的△A2B2C2 , 并写出A2点的坐标18. 如图,已知 是 的直径,弦 于点 , , .
(1)、画出△ABC绕点B逆时针旋转90°得到的△A1BC1 .(2)、以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△ABC放大后的△A2B2C2 , 并写出A2点的坐标18. 如图,已知 是 的直径,弦 于点 , , . (1)、求 ;(2)、求CD的长.19. 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,-1),DE=3.
(1)、求 ;(2)、求CD的长.19. 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,-1),DE=3.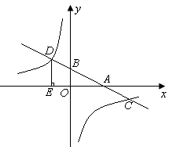 (1)、求反比例函数与一次函数的解析式.(2)、根据图象写出不等式kx+b> 的解集.(3)、连接OC、OD,求 的面积.20. 如图,某数学活动小组为测量一棵大树 和教学楼 的高,测角仪高 ,先在 处测得大树顶端 的仰角 为 ,此时教学楼顶端 恰好在视线 上,再向前走 到达 处 ,又测得教学楼顶端 的仰角 为 ,点 , , 三点在同一水平线上.
(1)、求反比例函数与一次函数的解析式.(2)、根据图象写出不等式kx+b> 的解集.(3)、连接OC、OD,求 的面积.20. 如图,某数学活动小组为测量一棵大树 和教学楼 的高,测角仪高 ,先在 处测得大树顶端 的仰角 为 ,此时教学楼顶端 恰好在视线 上,再向前走 到达 处 ,又测得教学楼顶端 的仰角 为 ,点 , , 三点在同一水平线上. (1)、求大树 的高;(2)、求教学楼 的高(结果保留根号).21. 如图, 为 的直径,点 是 上一点, 与 相切于点 ,过点 作 ,连接 , .
(1)、求大树 的高;(2)、求教学楼 的高(结果保留根号).21. 如图, 为 的直径,点 是 上一点, 与 相切于点 ,过点 作 ,连接 , . (1)、求证: 是 的角平分线;(2)、若 , ,求 的长.22. 某酒店试销售某种套餐,试销一段时间后发现,每份套餐的成本为7元,该店每天固定支出费用为200元(不含套餐成本).若每份售价不超过10元,每天可销售300份;若每份售价超过10元,每提高1元,每天的销售量就减少30份,设该店每份套餐的售价为 元( 为正整数),每天的销售量为 份,每天的利润为 元.(1)、直接写出 与 的函数关系式;(2)、求出 与 的函数关系式;并求出利润 的最大值.23. 如图,在边长为2的正方形 中,点 是射线 上一动点(点 不与点 重合),连接 , ,点 是线段 上一点,且 ,连接 .
(1)、求证: 是 的角平分线;(2)、若 , ,求 的长.22. 某酒店试销售某种套餐,试销一段时间后发现,每份套餐的成本为7元,该店每天固定支出费用为200元(不含套餐成本).若每份售价不超过10元,每天可销售300份;若每份售价超过10元,每提高1元,每天的销售量就减少30份,设该店每份套餐的售价为 元( 为正整数),每天的销售量为 份,每天的利润为 元.(1)、直接写出 与 的函数关系式;(2)、求出 与 的函数关系式;并求出利润 的最大值.23. 如图,在边长为2的正方形 中,点 是射线 上一动点(点 不与点 重合),连接 , ,点 是线段 上一点,且 ,连接 . (1)、求证: ;(2)、求证: ;(3)、求 的最小值.
(1)、求证: ;(2)、求证: ;(3)、求 的最小值.