吉林省长春市农安县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、 ±2 B、2 C、﹣2 D、16

查看试题解析
2. 下列实数中，最小的数是（）

A、 $- \sqrt{2}$ B、0 C、1 D、 $\sqrt[3]{8}$

查看试题解析
3. 计算（x³）²的结果是（）

A、x⁵ B、2x³ C、x⁹ D、x⁶

查看试题解析
4. 计算﹣3a·（2b），正确的结果是（）

A、﹣6ab B、6ab C、﹣ab D、ab

查看试题解析
5. 空气是混合物，为直观介绍空气各成分的百分比，最适合用的统计图是（）

A、折线图 B、条形图 C、直方图 D、扇形图

查看试题解析
6. 已知x²＋16x＋k是完全平方式，则常数k等于( )

A、64 B、48 C、32 D、16

查看试题解析
7. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（　　）

A、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、6，7，8 D、2，3，4

查看试题解析
8. 如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）

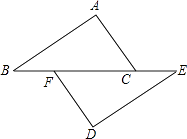A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC

查看试题解析
9. 如图，已知线段AB，分别以A，B为圆心，大于 $\frac{1}{2}$ AB为半径作弧，连接弧的交点得到直线l，在直线l上取一点C，使得∠CAB＝25°，延长AC至点M，则∠BCM的度数为（）

A、40° B、50° C、60° D、70°

查看试题解析
10. 如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 9的算术平方根是．

查看试题解析
12. $- 27$ 的立方根是．

查看试题解析
13. 一个矩形的面积为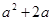，若一边长为，则另一边长为．

查看试题解析
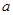14. 分解因式： $3 a^{2} - 3 b^{2} =$ .

查看试题解析
15. 已知2m－3n=－4，则代数式m(n－4)－n(m－6)的值为．

查看试题解析
16. 已知等腰三角形的一个内角为 50°，则顶角为.

查看试题解析
17. 某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图所示，那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为．

查看试题解析
18. 如图， $O C$ 为 $∠ A O B$ 的平分线. $C M ⊥ O B$ ， $O C = 5$ . $O M = 4$ .则点 $C$ 到射线 $O A$ 的距离为．

查看试题解析
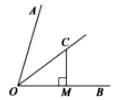19. 如图，AC、BD相交于点O， $∠ A = ∠ D$ ，请你再补充一个条件，使得 $△ AOB$ ≌ $△ DOC$ ，你补充的条件是．

查看试题解析
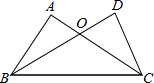20. 如图，在四边形ABCD中，AB∥DC，∠B=90⁰ ，连接AC∠DAC=∠BAC．若BC=4cm，AD=5cm，则AB=cm.

查看试题解析

三、解答题

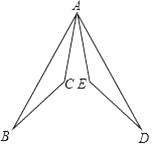
21. 先化简，再求值： $(x + 1) (x - 1) + {(2 x - 1)}^{2} - 2 x (2 x - 1)$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
22. 如图，已知AB=AD，AC=AE，∠BAE=∠DAC．
求证：∠C=∠E．

查看试题解析
23. 已知： $5^{a} = 3$ ， $5^{b} = 8$ ， $5^{c} = 72$ ．

(1)、求 ${(5^{a})}^{2}$ 的值．

(2)、求 $5^{a - b + c}$ 的值．

(3)、直接写出字母 $a$ 、 $b$ 、 $c$ 之间的数量关系．

查看试题解析
24. 如图，在直角 $△ A B C$ 中， $∠ C = 90^{\circ}$ ， $∠ C A B$ 的平分线 $A D$ 交 $B C$ 于点 $D$ ，若 $D E$ 垂直平分 $A B$ ，求 $∠ B$ 的度数．

查看试题解析
25. 某市中小学全面开展“阳光体育”活动，某校在大课间中开设了A：跳绳，B：跑操，C：舞蹈，D：健美操共四项活动，为了了解学生最喜欢哪一种活动，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：

(1)、这次被调查的学生共有人．

(2)、请将条形统计图补充完整．

(3)、求出扇形统计图中A项目对应的圆心角的度数．

查看试题解析
26.
如图，修公路遇到一座山，于是要修一条隧道．为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135°，BD=800米，求直线L上距离D点多远的C处开挖？（ $\sqrt{2}$ ≈1.414，精确到1米）

查看试题解析
27. 如图，在等边三角形 $A B C$ 中，点 $D$ ， $E$ 分别在边 $B C$ ， $A C$ 上，且 $D E // A B$ ，过点 $E$ 作 $E F ⊥ D E$ ，交 $B C$ 的延长线于点 $F$ ．

(1)、求 $∠ F$ 的度数；

(2)、若 $C D = 2$ ，求 $D F$ 的长．

查看试题解析
28. 完成下面问题：

(1)、问题发现：如图， $△ A C B$ 和 $△ D C E$ 均为等边三角形，点 $A$ ， $D$ ， $E$ 在同一直线上，连接 $B E$ ，填空：① $∠ A E B$ 的度数为；②线段 $A D$ ， $B E$ 之间的数量关系为；

(2)、拓展探究：如图， $△ A C B$ 和 $△ D C E$ 均为等腰直角三角形， $∠ A C B = ∠ D C E = 90 °$ ，点 $A$ ， $D$ ， $E$ 在同一直线上， $C M$ 为 $△ D C E$ 中 $D E$ 边上的高，连接 $B E$ ，请判断 $∠ A E B$ 的度数及线段 $C M$ ， $A E$ ， $B E$ 之间的数量关系，并说明理由．

查看试题解析