吉林省长春市宽城区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 若分式 在实数范围内有意义,则实数x的取值范围是( )A、x> B、x< C、x= D、x≠2. 下列运算正确的是( )A、 B、 C、 D、3. 某人将一枚质量分布均匀的硬币连续抛50次,落地后正面朝上30次,反面朝上20次,下列说法正确的是( )A、出现正面的频率是30 B、出现正面的频率是20 C、出现正面的频率是0.6 D、出现正面的频率是0.44. 用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设( )A、三角形中有一个内角小于或等于60° B、三角形中有两个内角小于或等于60° C、三角形中有三个内角小于或等于60° D、三角形中没有一个内角小于或等于60°5. 如图,AB=AC,点D、E分别是AB、AC上一点,AD=AE,BE、CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
 A、50° B、65° C、70° D、80°6. 如图,在△ABC中,∠C=90°,点D是线段AB的垂直平分线与BC的交点,连结AD.若CD=2,BD=4,则AC的长为( )
A、50° B、65° C、70° D、80°6. 如图,在△ABC中,∠C=90°,点D是线段AB的垂直平分线与BC的交点,连结AD.若CD=2,BD=4,则AC的长为( ) A、4 B、3 C、2 D、7. 如图,在△ 中, , 为钝角.按下列步骤作图:①以点B为圆心,适当长为半径作圆弧,交BC于点D,交AB于点E;②以点 为圆心, 长为半径作圆弧,交 于点 ;③以点 为圆心, 长为半径作圆弧,交②中所作的圆弧于点 ;④作射线 交 于点 .下列说法错误的是( )
A、4 B、3 C、2 D、7. 如图,在△ 中, , 为钝角.按下列步骤作图:①以点B为圆心,适当长为半径作圆弧,交BC于点D,交AB于点E;②以点 为圆心, 长为半径作圆弧,交 于点 ;③以点 为圆心, 长为半径作圆弧,交②中所作的圆弧于点 ;④作射线 交 于点 .下列说法错误的是( ) A、 = B、 =∠ACB C、∠CHB=∠A+∠B D、 =∠HCB8. 如图,∠EOF的顶点O是等边△ABC三条中线的交点,∠EOF的两边与△ABC的边交于E、F两点.若AB=4,∠EOF=120°,则∠EOF与△ABC的边所围成阴影部分的面积是( )
A、 = B、 =∠ACB C、∠CHB=∠A+∠B D、 =∠HCB8. 如图,∠EOF的顶点O是等边△ABC三条中线的交点,∠EOF的两边与△ABC的边交于E、F两点.若AB=4,∠EOF=120°,则∠EOF与△ABC的边所围成阴影部分的面积是( )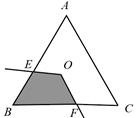 A、4 B、 C、2 D、
A、4 B、 C、2 D、二、填空题
-
9. 计算: = .10. 分解因式: = .11. 命题“等边三角形的每个内角都等于60°”的逆命题是命题.(填“真”或“假”)12. 如图,AB与CD相交于点O,OC=OD.若要得到△AOC≌△BOD,则应添加的条件是 . (写出一种情况即可)
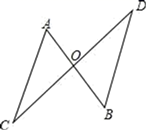 13. 如图,在△ABC中,AB=AC,BD是△ABC的一条角平分线,若∠A =36°,则∠BDC的度数为 .
13. 如图,在△ABC中,AB=AC,BD是△ABC的一条角平分线,若∠A =36°,则∠BDC的度数为 . 14. 如图,在△ABC中,∠ACB=90°,AC=BC.点D在斜边AB上,以CD为直角边作等腰直角三角形CDE,∠DCE=90°,连结BE.若AD=5,DB=12,则DE的长为 .
14. 如图,在△ABC中,∠ACB=90°,AC=BC.点D在斜边AB上,以CD为直角边作等腰直角三角形CDE,∠DCE=90°,连结BE.若AD=5,DB=12,则DE的长为 .
三、解答题
-
15. 计算: .16. 计算: .17. 如图,在8×6的正方形网格中,每个小正方形的顶点叫做格点,每个小正方形的边长都为1,△ABC的顶点都在格点上.
 (1)、AB的长为 , AC的长为 , △ABC是三角形(按角的分类填).(2)、在正方形网格中,画出所有与△ABC全等的△DBC.18. 如图,点C , E , F , B在同一直线上,点A , D在BC异侧,AB∥CD , AE=DF , ∠A=∠D .
(1)、AB的长为 , AC的长为 , △ABC是三角形(按角的分类填).(2)、在正方形网格中,画出所有与△ABC全等的△DBC.18. 如图,点C , E , F , B在同一直线上,点A , D在BC异侧,AB∥CD , AE=DF , ∠A=∠D .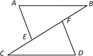 (1)、求证:AB=CD;(2)、若AB=CF , ∠B=40°,求∠D的度数.19. 2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.某市教育局发布了“普通中小学校劳动教育状况评价指标”,为了解某校学生一周劳动次数的情况,随机抽取若干学生进行调查,得到如下两幅不完整的统计图.请根据图中信息,解答下列问题:(1)、求这次调查活动共抽取的人数.(2)、直接写出m= , n= .(3)、请将条形统计图补充完整.
(1)、求证:AB=CD;(2)、若AB=CF , ∠B=40°,求∠D的度数.19. 2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.某市教育局发布了“普通中小学校劳动教育状况评价指标”,为了解某校学生一周劳动次数的情况,随机抽取若干学生进行调查,得到如下两幅不完整的统计图.请根据图中信息,解答下列问题:(1)、求这次调查活动共抽取的人数.(2)、直接写出m= , n= .(3)、请将条形统计图补充完整.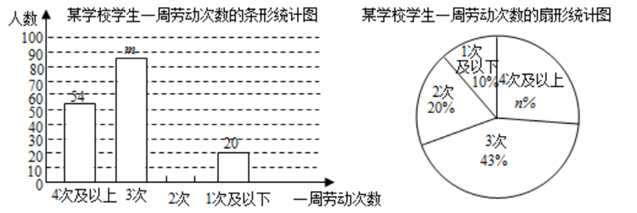 20. 观察下列等式:
20. 观察下列等式:, , .
将以上三个等式的两边分别相加,得:
.
(1)、直接写出计算结果: = .(2)、计算: .(3)、猜想并直接写出: = . (n为正整数)21. 如图,在一条东西走向河流的一侧有一村庄 河边原有两个取水点 其中 由于某种原因,由 到 的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点 在同一条直线上),并新修一条路 测得 千米, 千米, 千米. (1)、问 是否为从村庄 到河边的最近路.请通过计算加以说明;(2)、求新路 比原路 少多少千米.22. 如图,在△ABC中:
(1)、问 是否为从村庄 到河边的最近路.请通过计算加以说明;(2)、求新路 比原路 少多少千米.22. 如图,在△ABC中: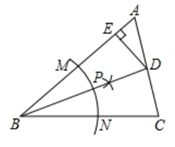 (1)、下列操作中,作∠ABC的平分线的正确顺序是(将序号按正确的顺序写在横线上).
(1)、下列操作中,作∠ABC的平分线的正确顺序是(将序号按正确的顺序写在横线上).①分别以点 M、N为圆心,大于 的长为半径作圆弧,在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于点N;
③画射线BP,交AC于点D.
(2)、连结MP、NP,通过证明△BMP≌△BNP,得到∠ABD=∠CBD,从而得到BD是∠ABC的平分线,其中证明△BMP≌△BNP的依据是(填序号)①SAS. ②ASA. ③AAS. ④SSS.
(3)、若AB=16,BC=14, ,过点D作DE⊥AB于E,求DE的长.23. 仔细阅读下面例题,解答问题.(例题)已知: ,求m、n的值.
解:∵ ,∴ ,
∴ ,∴ , ,∴ , .
∴m的值为4,n的值为4.
(问题)仿照以上方法解答下面问题:
(1)、已知 ,求x、y的值.(2)、在Rt△ABC中, ,三边长a、b、c都是正整数,且满足 ,求斜边长c的值.24. 如图,在长方形ABCD中,AB=4,BC=6.延长BC到点E,使CE=3,连结DE.动点P从点B出发,沿着BE以每秒1个单位的速度向终点E运动,点P运动的时间为t秒. (1)、DE的长为 .(2)、连结AP,求当t为何值时,△ABP≌△DCE.(3)、连结DP.①求当t为何值时,△PDE是直角三角形.②直接写出当t为何值时,△PDE是等腰三角形.
(1)、DE的长为 .(2)、连结AP,求当t为何值时,△ABP≌△DCE.(3)、连结DP.①求当t为何值时,△PDE是直角三角形.②直接写出当t为何值时,△PDE是等腰三角形.