吉林省长春市朝阳区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是（　　）

A、±3 B、3 C、±4.5 D、4.5

查看试题解析
2. 下列运算中，正确的是（）

A、 $a^{6} \div a^{2} = a^{3}$ B、 $- a^{2} \cdot a^{4} = a^{6}$ C、 ${(a b)}^{3} = a^{3} b^{3}$ D、 ${(a^{2})}^{4} = a^{6}$

查看试题解析
3. 小明5分钟内共投篮60次，共进球15个，则小明进球的频率是（）

A、0.25 B、60 C、0.26 D、15

查看试题解析
4. 下列各式从左到右的变形是因式分解的是（）

A、 $x^{2} + 2 x + 3 = {(x + 1)}^{2} + 2$ B、 $(x + y) (x - y) = x^{2} - y^{2}$ C、 $x^{2} - x y + y^{2} = {(x - y)}^{2} + x y$ D、 $2 x - 2 y = 2 (x - y)$

查看试题解析
5. 如图， $∠ C A D = ∠ B A D$ ，若依据“ASA”证明 $△ A C D ≌ △ A B D$ ，则需添加的一个条件是（）

A、 $∠ B = ∠ C$ B、 $∠ A D C = ∠ A D B$ C、 $A B = A C$ D、 $B D = C D$

查看试题解析
6. 如图，AB∥CD，AD＝CD，∠1＝70°，则∠2的度数是（）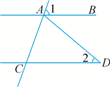

A、20° B、35° C、40° D、70°

查看试题解析
7. 若（-2x+a）（x-1）的展开式中不含x的一次项，则a的值是（）

A、-2 B、2 C、-1 D、任意数

查看试题解析
8. 如图，将长方形纸片ABCD沿AE折叠，使点D恰好落在BC边上点F处．若 $A B = 6$ ， $A D = 10$ ，则EC的长为（）

A、2 B、 $\frac{8}{3}$ C、3 D、 $\frac{10}{3}$

查看试题解析

二、填空题

9. 计算： $x \cdot x^{2} =$ ．

查看试题解析
10. 比较大小： $\sqrt{7}$ 3.

查看试题解析
11. 请举反例说明命题“对于任意实数x， $x^{2} + 6 x + 5$ 的值总是正数”是假命题，你举的反例是 $x =$ ．（写出一个值即可）

查看试题解析
12. 若 $x + y = 2 a$ ， $x - y = 2 b$ ，则 $x^{2} - y^{2}$ 的值为．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，AD平分 $∠ B A C$ ．若 $B C = 10$ ， $B D = 7$ ，则点D到AB的距离为．

查看试题解析
14. 如图，在 $5 \times 3$ 的正方形网格中， $△ A B C$ 的顶点均在格点上，则 $∠ A B C + ∠ A C B =$ ．

查看试题解析

三、解答题

15. 把下列多项式分解因式：

(1)、 $x^{2} - 4 x y + 4 y^{2}$

(2)、 $a (x - y) + b (x - y)$

查看试题解析
16. 先化简，再求值： $2 a (1 - 2 a) + (2 a + 1) (2 a - 1)$ ，其中 $a = 2$ ．

查看试题解析
17. 已知：图①、图②均为 $4 \times 4$ 的正方形网格，线段AB的端点均在格点上．

(1)、求线段AB的长．

(2)、分别在图①、图②中按要求以AB为腰画等腰 $△ A B C$ ，使点C也在格点上．
要求：在图①中画一个等腰锐角三角形 $△ A B C$ ．

在图②中画一个等腰直角三角形 $△ A B C$ ．

查看试题解析

18. 张老师计划通过步行锻炼身体，她用运动手环连续记录了6天的运动情况，并用统计表和统计图记录数据．

4月1日——4月6日张老师步行数据统计表

日期	4月1日	4月2日	4月3日	4月4日	4月5日	4月6日
步行数（步）	10672	4927	5543	6648
步行距离（公里）	6.8	3.1	3.5	4.6
卡路里消耗（千卡）	157	73	82	107
燃烧脂肪（克）	20	10	12	16

(1)、请你将手环记录的4月5日和4月6日的数据（如图①）填入表格．

(2)、请你将条形统计图（如图②）补充完整．

查看试题解析

19. 如图，在 $△ A B C$ 中， $A B = A C$ ，AD是BC边上的中线， $A E ⊥ B E$ 于点E，且 $B E = \frac{1}{2} B C$ ．求证：AB平分 $∠ E A D$ ．

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ，DE垂直平分AC．若 $∠ A = 30 °$ ，求 $∠ B C D$ 的度数．

查看试题解析
21. 已知 $a + b = 5$ ， $a b = 3$ ．

(1)、求 $a^{2} + b^{2}$ 的值．

(2)、求 $a - b$ 的值．

查看试题解析
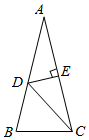22. 如图，点O是等边 $△ A B C$ 内一点，将CO绕点C顺时针旋转 $60 °$ 得到CD，连结OD，AO，AD．

(1)、求证： $△ B C O ≌ △ A C D$ ．

(2)、若 $∠ B O C = 150 °$ ， $O B = 8$ ， $O C = 6$ ，求 $△ A O D$ 的面积．

查看试题解析
23. （教材呈现）数学课上，赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法，方法如下：
如图， $∠ A O B$ 为已知角，试按下列步骤用直尺和圆规准确地作出 $∠ A O B$ 的平分线.

第一步：在射线OA、OB上，分别截取OD、OE，使 $O D = 0 E ；$

第二步：分别以点D和点E为圆心，适当长（大于线段DE长的一半）为半径作圆弧，在 $∠ A O B$ 内，两弧交于点C；

第三步：作射线OC.射线OC就是所要求作的 $∠ A O B$ 的平分线

(1)、赵老师用尺规作角平分线时，用到的三角形全等的判定方法是．

(2)、小明发现只利用直角三角板也可以作 $∠ A O B$ 的角平分线，方法如下：
步骤：①利用三角板上的刻度，在OA、OB上分别截取OM、ON，使 $O M = O N$ ．

②分别过点M、N作OM、ON的垂线，交于点P．

③作射线OP，则OP为 $∠ A O B$ 的平分线．

请根据小明的作法，求证OP为 $∠ A O B$ 的平分线．

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 5$ ， $B C = 3$ ，点P从点A出发，以每秒2个单位长度的速度沿折线 $A - C - B - A$ 运动．设点P的运动时间为t秒 $(t > 0)$ ．

(1)、求AC的长及斜边AB上的高．

(2)、当点P在CB上时，
①CP的长为（用含t的代数式表示）．

②若点P在 $∠ B A C$ 的角平分线上，则t的值为．

(3)、在整个运动过程中，直接写出 $△ B C P$ 是等腰三角形时t的值．

查看试题解析