吉林省白城市大安市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 小明有两根3cm、7cm的木棒，他想以这两根木棒为边做一个三角形，还需再选用的木棒长为（　　）

A、3cm B、4cm C、9cm D、10cm

查看试题解析
3. 如图，△ABC中，∠C＝80°，若沿图中虚线截去∠C，则∠1+∠2＝（）

A、360° B、260° C、180° D、140°

查看试题解析
4. 如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠A+∠P=（　　）

A、70° B、80° C、90° D、100°

查看试题解析
5. 下列各式从左到右的变形正确的是（）

A、 $\frac{y}{x} = \frac{y + 1}{x + 1}$ B、 $\frac{y}{x} = \frac{a y}{a x}$ C、 $\frac{y}{x} = \frac{a^{2} y}{a^{2} x}$ D、 $\frac{y}{x} = \frac{(a^{2} + 1) y}{(a^{2} + 1) x}$

查看试题解析
6. 甲乙两个码头相距 $s$ 千米，某船在静水中的速度为a千米/时，水流速度为b千米/时，则船一次往返两个码头所需的时间为（）小时.

A、 $\frac{2 s}{a + b}$ B、 $\frac{2 s}{a - b}$ C、 $\frac{s}{a} + \frac{s}{b}$ D、 $\frac{s}{a + b} + \frac{s}{a - b}$

查看试题解析

二、填空题

7.
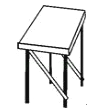
如图，李叔叔家的凳子坏了，于是他给凳子加了两根木条，这样凳子就比较牢固了，他所应用的数学原理是．

查看试题解析
8. 一个氧原子的直径为0.000000000148m，用科学记数法表示为m.

查看试题解析
9. 多边形每一个内角都等于108°，多边形一个顶点可引的对角线的条数是条．

查看试题解析
10. 若 $3^{x} = 4$ ， $9^{y} = 7$ ，则 $3^{x - 2 y}$ 的值为．

查看试题解析
11. 若25x²－mxy+9y²是完全平方式，则m的值为

查看试题解析
12. 如图，AC＝BC＝10 cm，∠B＝15°，若AD⊥BD于点D，则AD的长为．

查看试题解析
13. 如图，小明从A点出发，沿直线前进12米后向左转36°，再沿直线前进12米，又向左转36°…照这样走下去，他第一次回到出发地A点时，一共走了米．

查看试题解析
14. 一组按规律排列的式子： $\frac{2}{a}$ ， $- \frac{5}{a^{2}}$ ， $\frac{10}{a^{3}}$ ， $- \frac{17}{a^{4}}$ ， $\frac{26}{a^{5}}$ ，…，其中第7个式子是，第n个式子是（用含的n式子表示，n为正整数）．

查看试题解析

三、解答题

15. 如果一个多边形的内角和是外角和的3倍还多180°，那么这个多边形的边数是多少？

查看试题解析
16. 解方程： $\frac{3}{2 x - 2} + \frac{1}{1 - x} = 3$

查看试题解析
17. 因式分解：a²（x﹣y）+b²（y﹣x）

查看试题解析
18. 如图，D、E、F分别是△ABC的三条边上的点，CE＝BF，△DCE和△DBF的面积相等．求证：AD平分∠BAC．

查看试题解析
19. 先化简，再求值： $(\frac{x}{x^{2} + x} - 1) \div \frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ，其中x的值从不等式组 ${\begin{array}{l} - x \leq 1 \\ 2 x - 1 < 4 \end{array}$ 的整数解中选取．

查看试题解析
20. 如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0），C（﹣1，0）．

(1)、将△ABC向右平移5个单位，再向下平移4个单位得△A₁B₁C₁ ，图中画出△A₁B₁C₁ ，求平移后点A的对应点A₁的坐标．

(2)、将△ABC沿x轴翻折△A₂BC，图中画出△A₂BC，求翻折后点A对应点A₂坐标．

(3)、将△ABC向左平移2个单位，求△ABC扫过的面积．

查看试题解析
21. 如图，边长分别为a，b的两个正方形并排放在一起，请计算图中阴影部分面积，并求出当a+b=16，ab=60时阴影部分的面积.

查看试题解析
22. 已知：如图，在△ABC中，∠ABC＝3∠C，∠1＝∠2，BE⊥AE．求证：AC－AB＝2BE.

查看试题解析
23. 甲、乙两同学的家与学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校、乙同学骑自行车去学校．已知甲步行速度是乙骑自行车速度的 $\frac{1}{2}$ ，公交车的速度是乙骑自行车速度的2倍．甲乙两同学同时从家出发去学校，结果甲同学比乙同学早到2分钟．

(1)、求乙骑自行车的速度；

(2)、当甲到达学校时，乙同学离学校还有多远？

查看试题解析
24. （阅读理解）
课外兴趣小组活动时，老师提出了如下问题：

如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：

(1)、由已知和作图能得到△ADC≌△EDB的理由是_____.

A、SSS B、SAS C、AAS D、HL

(2)、求得AD的取值范围是______.

A、6＜AD＜8 B、6≤AD≤8 C、1＜AD＜7 D、1≤AD≤7

(3)、解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.
问题解决：

如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF.求证：AC＝BF.

查看试题解析
25. 某中学开学初在商场购进A、B两种品牌的足球，购买A品牌足球花费了2500元，购买B品牌足球花费了2000元，且购买A品牌的足球数量是购买B品牌足球数量的2倍，已知购买一个B品牌足球比购买一个A品牌足球多花30元

(1)、求购买一个A品牌、一个B品牌的足球各需多少元？

(2)、该中学响应习总书记足球进校园号召，决定两次购进A、B两种品牌足球共50个，恰逢商场对两种品牌足球的售价进行调整，A品牌足球售价比第一次购买时提高了8%，B品牌足球按第一次购买时售价的9折出售，如果这所中学此次购买A、B两种品牌足球的总费用不超过3240元，那么该中学此次最多可购买多少个B品牌足球？

查看试题解析
26. 如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．

(1)、若设AP＝x，则PC＝， QC＝；（用含x的代数式表示）

(2)、当∠BQD＝30°时，求AP的长；

(3)、在运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．

查看试题解析