黑龙江省伊春铁力市2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 下列运算中,计算结果正确的是( )A、 B、 C、 D、2. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 内角和等于外角和2倍的多边形是( )
3. 内角和等于外角和2倍的多边形是( )
A、五边形 B、六边形 C、七边形 D、八边形4. 等腰三角形的一个内角为50°,则另外两个角的度数分别为( )A、65°,65° B、50°,80° C、65°,65°或50°,80° D、50°,50°5. 下列运算中正确的是( )A、 B、 C、 D、6. 在式子 , , , , , 中,分式的个数是( )A、2 B、3 C、4 D、57. 计算 ( )A、2 B、 C、 D、38. 到三角形的三个顶点距离相等的点是( )A、三条角平分线的交点 B、三条边的垂直平分线的交点 C、三条高的交点 D、三条中线的交点9. 若 是完全平方式,则 的值是( )A、22 B、44 C、±44 D、±2210. 若点 与 关于 轴对称,则( )A、 , B、 , C、 , D、 ,11. 在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )A、4个 B、3个 C、2个 D、1个12. 如图,△ABC中,AB=5,AC=8,BD,CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,分别交AB,AC于E,F,则△AEF的周长为 ( )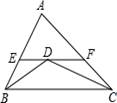 A、12 B、13 C、14 D、1813. 如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF度数是( )
A、12 B、13 C、14 D、1813. 如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF度数是( )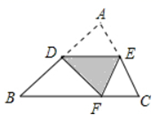 A、80° B、70° C、60° D、不确定
A、80° B、70° C、60° D、不确定二、填空题
-
14. 如图: , , ,若 ,则 等于.
 15. 已知等腰三角形一腰上的高与另一腰的夹角为50°,则等腰三角形的顶角度数为 .16. 如图, 分别是△ABC 的高和角平分线,且 , 则 的度数为 .
15. 已知等腰三角形一腰上的高与另一腰的夹角为50°,则等腰三角形的顶角度数为 .16. 如图, 分别是△ABC 的高和角平分线,且 , 则 的度数为 .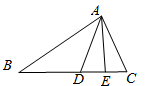 17. 计算 = .18. 如果分式 有意义,那么x的取值范围是 .19. 若关于 的分式方程 无解,则 .20. 因式分解: .21. 计算: = .22. 三角形有两条边的长度分别是5和7,则第三边a的取值范围是 .23. 在△ABC中,高AD和BE所在直线交于点H,且BH=AC,则∠ABC= .
17. 计算 = .18. 如果分式 有意义,那么x的取值范围是 .19. 若关于 的分式方程 无解,则 .20. 因式分解: .21. 计算: = .22. 三角形有两条边的长度分别是5和7,则第三边a的取值范围是 .23. 在△ABC中,高AD和BE所在直线交于点H,且BH=AC,则∠ABC= .三、解答题
-
24. 分解因式:(1)、 ;(2)、 .(3)、解方程: .(4)、计算25. 化简,再求值: ,其中x=226. 在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形 (三角形的三个顶点都在小正方形的顶点上)
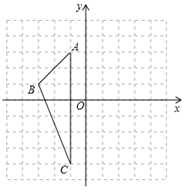 (1)、写出 的面积;(2)、画出 关于 轴对称的 ;(3)、写出点 及其对称点 的坐标.27. 已知:如图,BC∥EF,AB=DE,BC=EF,求证:∠C=∠F.
(1)、写出 的面积;(2)、画出 关于 轴对称的 ;(3)、写出点 及其对称点 的坐标.27. 已知:如图,BC∥EF,AB=DE,BC=EF,求证:∠C=∠F.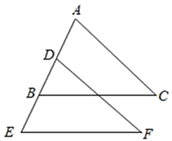 28. 八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达,已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.29. 如图1,点P、Q分别是等边 上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
28. 八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达,已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.29. 如图1,点P、Q分别是等边 上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M. (1)、求证: ;(2)、当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
(1)、求证: ;(2)、当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.