黑龙江省绥化市绥棱县2020-2021学年八年级上学期数学期末试卷（五四学制）

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算中正确的是（）

A、 $a^{5} + a^{5} = 2 a^{10}$ B、 $3 a^{3} \cdot 2 a^{2} = 6 a^{6}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 ${(- 2 a b)}^{2} = 4 a^{2} b^{2}$

查看试题解析
3. 一个等腰三角形的两边长分别为4，8，则它的周长为（）.

A、12 B、16 C、16或20 D、20

查看试题解析
4.
如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（　　）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
5. 如图，将四边形纸片ABCD沿AE向上折叠，使点B落在DC边上的点F处 $.$ 若 $△ AFD$ 的周长为18， $△ ECF$ 的周长为6，四边形纸片ABCD的周长为 $($ $)$

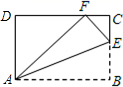A、20 B、24 C、32 D、48

查看试题解析
6. 如果将分式 $\frac{2 x}{x + y}$ 中的字母x与y的值分别扩大为原来的10倍，那么这个分式的值（）

A、扩大为原来的10倍 B、扩大为原来的20倍 C、缩小为原来的 $\frac{1}{10}$ D、不改变

查看试题解析
7. 一艘轮船由海平面上A地出发向南偏西40°的方向行驶80海里到达B地，再由B地向北偏西20°的方向行驶80海里到达C地，则A，C两地相距（）

A、100海里 B、80海里 C、60海里 D、40海里

查看试题解析
8. 如图，在△ABC中，AB＝AC，D为BC上一点，且DA＝DC，BD＝BA，则∠B的大小为（）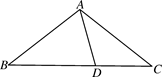

A、40° B、36° C、30° D、25°

查看试题解析
9. 如图，根据计算正方形ABCD的面积，可以说明下列哪个等式成立（）

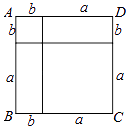A、（a﹣b）²=a²﹣2ab+b² B、（a+b）²=a²+2ab+b² C、（a+b）（a﹣b）=a²﹣b² D、a（a﹣b）=a²﹣ab

查看试题解析
10. 某中学为了创建“最美校园图书屋”，新购买了一批图书，其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍.已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本，那么学校购买文学类图书平均每本书的价格是多少元?设学校购买文学类图书平均每本书的价格是x元，则下面所列方程中正确的是（）

A、 $\frac{12000}{x + 100} = \frac{12000}{1.2 x}$ B、 $\frac{12000}{x} = \frac{12000}{1.2 x} + 100$ C、 $\frac{12000}{x - 100} = \frac{12000}{1.2 x}$ D、 $\frac{12000}{x} = \frac{12000}{1.2 x} - 100$

查看试题解析

二、填空题

11. 新型冠状病毒的直径约为125纳米，1毫米=1000000纳米，125纳米用科学记数法表示为毫米．

查看试题解析
12. 分解因式： $x^{3} - 4 x$ =

查看试题解析
13. 如图，点B、F、C、E在一条直线上，已知BF=CE，AC∥DF，请你添加一个适当的条件，使得△ABC≌△DEF．

查看试题解析
14. 要使式子 $\frac{4}{x - 2}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
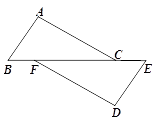15. 若一个多边形的内角和与外角和之和是1800°，则此多边形是边形.

查看试题解析
16. 已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40^o ，则此等腰三角形的顶角度数为

查看试题解析
17. 如果 $x^{2} + k x y + 36 y^{2}$ 是完全平方式，则k的值是．

查看试题解析
18. 将一副三角板按图中方式叠放，那么两条最长边所夹锐角的度数是．

查看试题解析
19. 如图所示，小华从A点出发，沿直线前进10米后左转24°，再沿直线前进10米，又向左转24°，…，照这样走下去，他第一次回到出发地A点时，一共走的路程是

查看试题解析
20. 如图所示，在 $△ A B C$ 中， $∠ A = 80 °$ ，延长 $B C$ 到 $D$ ， $∠ A B C$ 与 $∠ A C D$ 的平分线相交于 $A_{1}$ 点， $∠ A_{1} B C$ 与 $∠ A_{1} C D$ 的平分线相交于 $A$ 点，依此类推， $∠ A_{4} B C$ 与 $∠ A_{4} C D$ 的平分线相交于 $A_{5}$ 点，则 $∠ A_{5}$ 的度数是．

查看试题解析

三、解答题

21. 先化简，再求值： $\frac{a^{2} - b^{2}}{a^{2} - a b} \div (a + \frac{2 a b + b^{2}}{a})$ ，其中 $a = - 2$ ， $b = 3$ .

查看试题解析
22. 解分式方程： $\frac{3}{x^{2} - x}$ +1= $\frac{x}{x - 1}$ ．

查看试题解析
23. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点分别为 $A (2 ， 3)$ ， $B (3 ， 1)$ ， $C (- 2 ， - 2)$ ．

(1)、请在图中作出 $△ A B C$ 关于 $y$ 轴的轴对称图形 $△ A^{'} B^{'} C^{'}$ （ $A$ ， $B$ ， $C$ 的对称点分别是 $A^{'}$ ， $B^{'}$ ， $C^{'}$ ），并直接写出 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标．

(2)、求 $△ A^{'} B^{'} C^{'}$ 的面积．

查看试题解析
24. 如图，已知 $△ A B C$ 中， $A B = A C$ ，点 $P$ 在 $B C$ 上．

(1)、试用直尺和圆规在 $A C$ 上找一点 $D$ ，使 $∠ C P D = ∠ B A P$ （不写作法，但需保留作图痕迹）；

(2)、在（1）的条件下，若 $∠ A P C = 2 ∠ A B C$ ；求证： $P D // A B$ ．

查看试题解析
25. 问题探索：

(1)、已知一个分数 $\frac{n}{m} (m > n > 0)$ ，如果分子、分母同时增加1，分数的值是增大还是减小?请说明你的理由.

(2)、若正分数 $\frac{n}{m} (m > n > 0)$ 中分子和分母同时增加2，3，…，k（整数k>0），情况如何?

(3)、请你用上面的结论解释下面的问题：
建筑学规定：民用住宅窗户面积必须小于地板面积，但按采光标准，窗户面积与地板面积的比应不小于10%，并且这个比值越大，住宅的采光条件越好，问：同时增加相等的窗户面积和地板面积，住宅的采光条件是变好了，还是变坏了?请说明理由.

查看试题解析
26. 问题引入：

(1)、如图①所示， $△ A B C$ 中，点 $O$ 是 $∠ A B C$ 和 $∠ A C B$ 的平分线的交点，若 $∠ A = α$ ，则 $∠ B O C =$ （用 $α$ 表示）；不用说明理由，直接填空．
如图②所示， $∠ O B C = \frac{1}{3} ∠ A B C$ ， $∠ O C B = \frac{1}{3} ∠ A C B$ ，若 $∠ A = α$ ，则 $∠ B O C =$ （用 $α$ 表示）不用说明理由，直接填空．

(2)、如图③所示， $∠ O B C = \frac{1}{3} ∠ D B C$ ， $∠ O C B = \frac{1}{3} ∠ E C B$ ，若 $∠ A = α$ ，求 $∠ B O C$

查看试题解析
27. 东营市某学校2015年在商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元．

(1)、求购买一个甲种足球、一个乙种足球各需多少元；

(2)、2016年为响应习总书记“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个，恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%，如果此次购买甲、乙两种足球的总费用不超过2900元，那么这所学校最多可购买多少个乙种足球？

查看试题解析
28. 如图，在平面直角坐标系中，点 $A$ 、 $B$ 分别在 $x$ 、 $y$ 轴上，已知点 $B$ 的坐标为 $(0 ， 1)$ ，且 $∠ B O A = 30^{\circ}$ .

(1)、求 $A B$ 的长度；

(2)、以 $A B$ 为一边作等边，过点 $A$ 作 $A D ⊥ A B$ ，交 $O A$ 的垂直平分线 $M N$ 于点 $D$ .求证： $B D = O E$ ；

(3)、在（2）的条件下，连接 $D E$ 交 $A B$ 于 $F$ ，求证： $F$ 为 $D E$ 的中点.

查看试题解析