北京市延庆区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 2020年初,新型冠状病毒引发肺炎疫情.一方有难,八方支援,危难时刻,全国多家医院纷纷选派医护人员驰援武汉.下面是四家医院标志的图案部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、3. 一个不透明的盒子中装有3个白球、9个红球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的可能性是( )A、 B、 C、 D、4. 下列长度的三条线段,能组成直角三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,12,135. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、
2. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、3. 一个不透明的盒子中装有3个白球、9个红球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的可能性是( )A、 B、 C、 D、4. 下列长度的三条线段,能组成直角三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,12,135. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、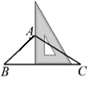 B、
B、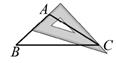 C、
C、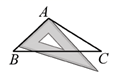 D、
D、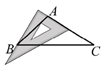 6. 北京今年6月某日部分区县的高气温如下表:
6. 北京今年6月某日部分区县的高气温如下表:区县 大兴 通州 平谷 顺义 怀柔 门头沟 延庆 昌平 密云 房山 最高气温 32 32 30 32 30 32 29 32 30 32 则这10个区县该日最高气温的众数和中位数分别是( )
A、32,32 B、32,30 C、30,32 D、32,317. 在Rt△ABC中,∠ACB=90°,AC=BC=1.点Q在直线BC上,且AQ=2,则线段BQ的长为( )A、 B、 C、 或 D、 或8. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( ) A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,4
A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,4二、填空题
-
9. 要使分式 有意义,则 的取值范围是 .10. 化简: = .11. 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,AB=10,AD=5,AC=4,则△ABD的面积为 .
 12. 如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=20°,且AE=AD,则∠CDE的度数是 .
12. 如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=20°,且AE=AD,则∠CDE的度数是 . 13. 如图,在 中,AB的垂直平分线交A于点D , 交BC于点E , 若 , ,则 的周长为 .
13. 如图,在 中,AB的垂直平分线交A于点D , 交BC于点E , 若 , ,则 的周长为 . 14. 如图,△ABC是等边三角形,边长为2,AD是BC边上的高.E是AC边中点,点P是AD上的一个动点,则PC+PE的最小值是 ,此时∠CPE的度数是 .
14. 如图,△ABC是等边三角形,边长为2,AD是BC边上的高.E是AC边中点,点P是AD上的一个动点,则PC+PE的最小值是 ,此时∠CPE的度数是 . 15. 如图,在长方形 的对称轴 上找点 ,使得 , 均为等腰三角形,则满足条件的点 有个.
15. 如图,在长方形 的对称轴 上找点 ,使得 , 均为等腰三角形,则满足条件的点 有个.
三、解答题
-
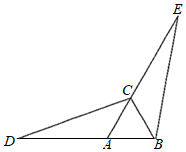
16. 计算: .17. 计算: .18. 如图,已知等边三角形ABC , 延长BA至点D , 延长AC至点E , 使AD=CE , 连接CD , BE . 求证:△ACD≌△CBE .
 19. 解分式方程: .20. 先化简,再求值: ,其中 .21. 北京延庆于2020年12月1日6时26分迎来首列高铁G8881停靠标志着京张高铁延庆支线及市郊铁路S2线正式开通运营,综合交通服务中心(换乘中心)同步投入使用.作为京张高铁支线火车站,延庆综合交通服务中心是集高铁、市郊铁路、公交、出租车、自行车及停车场等多种形式于一体的综合枢纽.同时,作为北京2022年冬奥会重点交通服务配套设施,该中心将在冬奥会期间承担观众和部分注册人员的交通转换及服务功能,冬奥会后将服务于延庆区日常活动及通勤,并为游客提供出行便利.小李计划周末到延庆站参观.为了响应绿色出行号召,他从家到延庆站由驾车改为骑自行车.小李家距离延庆站20千米,在相同路线上,驾车的平均速度是骑自行车平均速度的4倍,骑自行车所用时间比驾车所用时间多45分钟,求小李驾车的平均速度是多少?22. 已知:如图,线段AB和射线BM交于点B.
19. 解分式方程: .20. 先化简,再求值: ,其中 .21. 北京延庆于2020年12月1日6时26分迎来首列高铁G8881停靠标志着京张高铁延庆支线及市郊铁路S2线正式开通运营,综合交通服务中心(换乘中心)同步投入使用.作为京张高铁支线火车站,延庆综合交通服务中心是集高铁、市郊铁路、公交、出租车、自行车及停车场等多种形式于一体的综合枢纽.同时,作为北京2022年冬奥会重点交通服务配套设施,该中心将在冬奥会期间承担观众和部分注册人员的交通转换及服务功能,冬奥会后将服务于延庆区日常活动及通勤,并为游客提供出行便利.小李计划周末到延庆站参观.为了响应绿色出行号召,他从家到延庆站由驾车改为骑自行车.小李家距离延庆站20千米,在相同路线上,驾车的平均速度是骑自行车平均速度的4倍,骑自行车所用时间比驾车所用时间多45分钟,求小李驾车的平均速度是多少?22. 已知:如图,线段AB和射线BM交于点B. (1)、利用尺规完成以下作图,并保留作图痕迹(不写作法)
(1)、利用尺规完成以下作图,并保留作图痕迹(不写作法)①在射线BM上作一点C,使AC=AB,连接AC;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
(2)、在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.23. 我们规定用(a,b)表示一对数对.给出如下定义:记 , ,其中(a > 0,b > 0),将(m,n)与(n,m)称为数对(a,b)的一对“对称数对”.例如:(4,1)的一对“对称数对”为( ,1)和(1, );
(1)、数对(9,3)的一对“对称数对”是;(2)、若数对(3,y)的一对“对称数对”相同,则y的值为;(3)、若数对(x,2)的一个“对称数对”是( ,1),则x的值为;(4)、若数对(a,b)的一个“对称数对”是( , ),求ab的值.24. 在△ABC中,AB=AC,D,E分别是边BC上的两点,AD=AE,点E关于直线AC的对称点是点M,连接AM,DM;(1)、如图1,当∠BAC=60°时;
①依题意补全图形;
②若∠BAD= ,求∠AEB的大小(用含 的式子表示);
③求证:DA=DM;
(2)、如图2,当∠BAC=90°时,依题意补全图形,用等式表示线段DC,EC,AM之间的数量关系,并证明.