北京市通州区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 当 $x = 1$ 时，下列分式没有意义的是（）

A、 $\frac{x + 1}{x}$ B、 $\frac{x}{x - 1}$ C、 $\frac{x - 1}{x}$ D、 $\frac{x}{x + 1}$

查看试题解析
2. 下列体育运动图案中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列语句中正确的是（）

A、16的算术平方根是±4 B、任何数都有两个平方根 C、∵3的平方是9，∴9的平方根是3 D、﹣1是1的平方根

查看试题解析
4. 下列事件中，属于随机事件的是（）

A、用长度分别是4cm，4cm，9cm的细木条首尾顺次相连可组成一个等腰三角形 B、以长度分别是5cm，4cm，3cm的线段为三角形三边，能构成直角三角形 C、分式的分子、分母同乘一个不等于零的整式，分式的值不变 D、任意画一个三角形，恰好是同一条边上的高线与中线重合

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{{(- 4)}^{2}}$ =2 B、（ $\sqrt{2}$ ）²=4 C、 $\sqrt{2}$ × $\sqrt{5}$ = $\sqrt{10}$ D、 $\sqrt{6}$ ÷ $\sqrt{2}$ =3

查看试题解析
6. 如图，点E，点F在直线AC上，AF＝CE，AD＝CB，下列条件中不能推断 $△$ ADF≌ $△$ CBE的是（）

A、∠D＝∠B B、∠A＝∠C C、BE＝DF D、AD∥BC

查看试题解析
7. 小明学了在数轴上表示无理数的方法后，进行了练习：首先画数轴，原点为O，在数轴上找到表示数2的点A，然后过点A作AB⊥OA，使AB＝1；再以O为圆心，OB的长为半径作弧，交数轴正半轴于点P，那么点P表示的数是（）

A、2.2 B、 $\sqrt{5}$ C、 $1 + \sqrt{2}$ D、 $\sqrt{6}$

查看试题解析
8. 如图，在 $△$ ABC中，∠ACB＝90°，边BC的垂直平分线EF交AB于点D，连接CD，如果CD＝6，那么AB的长为（）

A、6 B、3 C、12 D、4.5

查看试题解析
9. 某校为了解学生的课外阅读情况，随机抽取了一个班级的学生，对他们一周的读书时间进行了统计，统计数据如表所示：

读书时间（小时）

7

8

9

10

11

学生人数

6

10

9

8

7

关于该班学生一周读书时间的数据有下列说法：①一周读书时间数据的中位数是9小时；②一周读书时间数据的众数是8小时；③一周读书时间数据的平均数是9小时；④一周读书时间不少于9小时的人数占抽查学生的50%．其中说法正确的序号是（）

A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析
10. 如图，在Rt $△$ ABC中，∠BAC＝90°，以点A为圆心，以AB长为半径作弧交BC于点D，再分别以点B，D为圆心，以大于 $\frac{1}{2} B D$ 的长为半径作弧，两弧交于点P，作射线AP交BC于点E，如果AB＝3，AC＝4，那么线段AE的长度是（）

A、 $\frac{12}{5}$ B、 $\frac{9}{5}$ C、 $\frac{8}{5}$ D、 $\frac{7}{5}$

查看试题解析

二、填空题

11. 如果 ${(\sqrt{m})}^{2} = 3$ ，那么m的值是．

查看试题解析
12. 一个不透明的盒子中装有2个红球，1个白球和1个黄球，它们除颜色外都相同，如果从中任意摸出一个球，那么摸到红球的可能性大小是．

查看试题解析
13. 计算 $\frac{m}{m^{2} - 1} - \frac{1}{1 - m^{2}}$ ，的符合题意结果为．

查看试题解析
14. 如图，已知∠ABC=∠BAD，添加一个条件使△ABC≌△BAD，你添加的条件是

查看试题解析
15. 用一个 $a$ 的值说明命题“如果 $a^{2} \geq 1$ ，那么 $a \geq 1$ ”是错误的，这个值可以是a＝．

查看试题解析
16. 已知 $\sqrt{3 + a} + {(b - 2)}^{2} = 0$ ，那么a+b的值为．

查看试题解析
17. 如图中的每个小方格都是边长为1的正方形，那么∠ABC的度数是．

查看试题解析
18. 数学课上，同学们兴致勃勃地尝试着利用不同画图工具画一个角的平分线．小明用直尺画角平分线的方法如下：
①用直尺的一边贴在∠AOB 的OA边上，沿着直尺的另一条边画直线m；

②再用直尺的一边贴在∠AOB 的OB边上，沿着直尺的另一条边画直线n，直线m与直线n交于点D；

③作射线OD．射线OD是∠AOB的平分线．

请回答：小明的画图依据是．

查看试题解析
19. 某校为了丰富学生的校园生活，准备购买一批陶笛．已知A型陶笛比B型陶笛的单价低20元，用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同，设A型陶笛的单价为 $x$ 元，根据题意列出正确的方程是．

查看试题解析
20. 给出下列对应的表格：

a

0.0001

0.01

1

100

10000

$\sqrt{a}$

0.01

0.1

1

10

100

利用表格中的规律计算：已知 $\sqrt{15} = k$ ， $\sqrt{0.15} = m$ ， $\sqrt{1500} = n$ ，那么 $m + n$ = ．（用含k的代数式表示）

查看试题解析

三、解答题

21. 计算： ${(π - 3)}^{0} - \sqrt{9} + \sqrt[3]{- 8} + | 1 - \sqrt{3} |$

查看试题解析
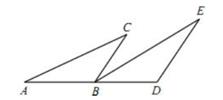
22. 解方程： $\frac{1 - x}{2 - x} = \frac{1}{x - 2} + 3$ ．

查看试题解析
23. 如图，点B在线段AD上，BC∥DE，AB=ED，BC=DB。求证：∠A=∠E。

查看试题解析
24. 计算： $\sqrt{48} - 6 \sqrt{\frac{1}{3}} + (2 \sqrt{3} - 2) (2 \sqrt{3} + 2)$ ．

查看试题解析
25. 已知 $a = \sqrt{2} - 1$ ，求代数式 $\frac{2 a - 4}{a^{2} - 1} \div (1 - \frac{1}{a - 1})$ 的值．

查看试题解析
26. 如图，在 $△$ ABC中，BD平分∠ABC，E是BD上一点，EA⊥AB，且EB＝EC．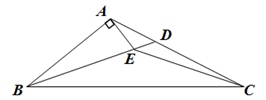

(1)、如果∠ABC＝40°，求∠DEC的度数；

(2)、求证：BC＝2AB．

查看试题解析
27. 为了解某校八年级学生的物理和生物实验操作情况，随机抽查了40名同学实验操作的得分（满分为10分）．根据获取的样本数据，制作了下面的条形统计图和扇形统计图，请根据相关信息，解答下列问题．

(1)、这40个样本数据平均数是，众数是，中位数是；

(2)、扇形统计图中m的值为；扇形统计图中“6分”所对的圆心角的度数是；

(3)、若该校八年级共有480名学生，估计该校物理和生物实验操作得满分的学生有多少人．

查看试题解析
28. 下面是小明同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程．
已知：如图1，直线 $l$ 和直线 $l$ 外一点P．

求作：直线PQ，使直线PQ∥直线 $l$ ．

作法：如图2，

①在直线 $l$ 上取一点A，连接PA；

②作PA的垂直平分线MN，分别交直线 $l$ ，线段PA于点B，O；

③以O为圆心，OB长为半径作弧，交直线MN于另一点Q；

④作直线PQ，所以直线PQ为所求作的直线．

根据上述作图过程，回答问题：

(1)、用直尺和圆规，补全图2中的图形（保留作图痕迹）；

(2)、完成下面的证明：
证明：∵直线MN是PA的垂直平分线，

∴ $P O =______$ ， $∠ P O Q =_______= 90 °$ ，

∵ $O Q =______$ ，

∴ $△ P O Q ≌ △ A O B$ ．

∴ $_______=________$ ．

∴PQ∥ $l$ （ ▲ ）（填推理的依据）．

查看试题解析
29. 如图，将 $△$ ABC绕点B顺时针旋转90°得到 $△$ DBE（点A，点C的对应点分别为点D，点E）．

(1)、根据题意补全图形；

(2)、连接DC，CE，如果∠BCD＝45°．用等式表示线段DC，CE，AC之间的数量关系，并证明．

查看试题解析
30. 如图，在等边三角形ABC右侧作射线CP，∠ACP= $α$ （0°< $α$ <60°），点A关于射线CP的对称点为点D，BD交CP于点E，连接AD，AE．

(1)、依题意补全图形；

(2)、求∠DBC的大小（用含 $α$ 的代数式表示）；

(3)、直接写出∠AEB的度数；

(4)、用等式表示线段AE，BD，CE之间的数量关系，并证明．

查看试题解析

读书时间（小时）	7	8	9	10	11
学生人数	6	10	9	8	7

a	0.0001	0.01	1	100	10000
$\sqrt{a}$	0.01	0.1	1	10	100