初中数学湘教版八年级下册2.6.2菱形的判定 同步练习
试卷更新日期:2021-03-12 类型:同步测试
一、单选题
-
1. 在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )A、BC=CD B、AB=CD C、∠D=90° D、AD=BC2. 下列条件中,不能判定四边形ABCD为菱形的是( ).A、AC⊥BD,AC与BD互相平分 B、AB=BC=CD=DA C、AB=BC,AD=CD,且AC⊥BD D、AB=CD,AD=BC,AC⊥BD3. 如图,某同学作线段AB的垂直平分线:分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点C,D,则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是( )
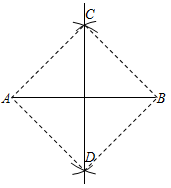 A、菱形 B、平行四边形 C、矩形 D、一般的四边形4. 如图,若要使平行四边形ABCD成为菱形,需添加的条件是( )
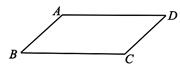
A、菱形 B、平行四边形 C、矩形 D、一般的四边形4. 如图,若要使平行四边形ABCD成为菱形,需添加的条件是( )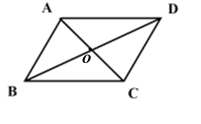 A、 B、 C、 D、 互相垂直5. 如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:
A、 B、 C、 D、 互相垂直5. 如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:甲:以B , A为圆心,AB长为半径作弧,分别交BC , AD于点E , F , 则四边形ABEF为菱形;乙:作∠A , ∠B的平分线AE , BF , 分别交BC于点E , 交AD于点F , 则四边形ABEF是菱形;关于甲、乙两人的画法,下列判断正确的是( )
 A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误6. 如图, 中, 平分 , 交 于 , 交 于 ,若 ,则四边形 的周长是( )
A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误6. 如图, 中, 平分 , 交 于 , 交 于 ,若 ,则四边形 的周长是( )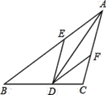 A、24 B、28 C、32 D、367. 有两张宽为3,长为9的矩形纸片如图所示叠放在一起,使重叠的部分构成一个四边形,则四边形的最大面积是( )
A、24 B、28 C、32 D、367. 有两张宽为3,长为9的矩形纸片如图所示叠放在一起,使重叠的部分构成一个四边形,则四边形的最大面积是( ) A、27 B、12 C、15 D、188. 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A、27 B、12 C、15 D、188. 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )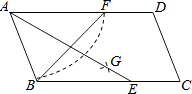 A、16 B、15 C、14 D、139. 如图,是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:对于甲、乙两人的作法,可判断( )
A、16 B、15 C、14 D、139. 如图,是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:对于甲、乙两人的作法,可判断( ) A、甲、乙均正确 B、甲、乙均错误 C、甲正确,乙错误 D、甲错误,乙正确10. 将一矩形纸片对折后再对折,如图1、图2,然后沿图3中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形一定是( ).
A、甲、乙均正确 B、甲、乙均错误 C、甲正确,乙错误 D、甲错误,乙正确10. 将一矩形纸片对折后再对折,如图1、图2,然后沿图3中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形一定是( ).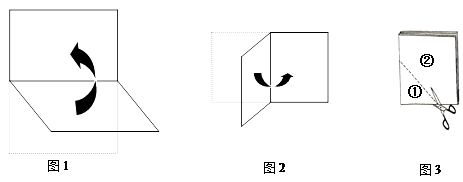 A、平行四边形 B、矩形 C、菱形 D、正方形
A、平行四边形 B、矩形 C、菱形 D、正方形二、填空题
-
11.
如图,在菱形ABCD中,∠A=45°,DE⊥AB,垂足为E,若CD=4cm,则菱形ABCD的面积是 cm2 .
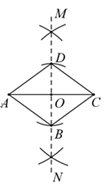
 12. 已知:线段 AC , 如图.
12. 已知:线段 AC , 如图.
求作:以线段 AC 为对角线的一个菱形 ABCD .
作法:
①作线段AC的垂直平分线MN交AC 点于O;
②以点O为圆心,任意长为半径画弧,交直线MN于点B , D;
③顺次连结点A , B , C , D , 则四边形ABCD即为所求作的菱形.
请回答:上面尺规作图作出菱形 ABCD的依据是 .
 13. 如图,平行四边形 的两条对角线 相交于点 , , , ,则四边形 的形状是.
13. 如图,平行四边形 的两条对角线 相交于点 , , , ,则四边形 的形状是.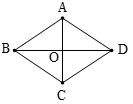 14. 如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=°.
14. 如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=°.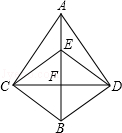 15. 如图,已知:在▱ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
15. 如图,已知:在▱ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.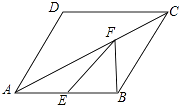
▱ABCD的周长是;
EF+BF的最小值为 .
三、解答题
-
16. 如图,▱ABCD中对角线BD平分∠ABC.
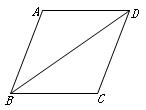
求证:▱ABCD是菱形.
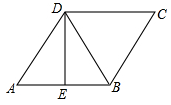
17. 已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.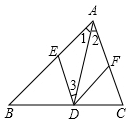 18. 如图,在Rt△ABC.∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.
18. 如图,在Rt△ABC.∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.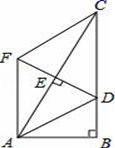 19. 如图,在 中,∠ACB=90⁰,∠B=60⁰,作边AC的垂直平分线 交AB于点D,过点C作AB的平行线交 于点E,判断四边形DBCE的形状,并说明理由.
19. 如图,在 中,∠ACB=90⁰,∠B=60⁰,作边AC的垂直平分线 交AB于点D,过点C作AB的平行线交 于点E,判断四边形DBCE的形状,并说明理由.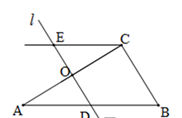
四、综合题
-
20. 如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE.
 (1)、求证:四边形BDCE是菱形;(2)、若AD=8,BD=6,求菱形BDCE的面积.
(1)、求证:四边形BDCE是菱形;(2)、若AD=8,BD=6,求菱形BDCE的面积.