北京市平谷区2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-12 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{a - 1}$ 中，字母a的取值范围是（　　）

A、a＜1 B、a≤1 C、a≥1 D、a＞1

查看试题解析
2. 如果分式 $\frac{m - 1}{m + 1}$ 的值为零，则 $m$ 的值是（）

A、 $m = - 1$ B、 $m = 1$ C、 $m = \pm 1$ D、 $m = 0$

查看试题解析
3. 我国民间，流传着许多含有吉祥意义的图案，表示对幸福生活的向往，良辰佳节的祝贺.比如下列图案分别表示“福”“禄”“寿”“喜”，其中是轴对称图形的有几个（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 已知三角形的两边长分别为5和7，则第三边的中线长x的取值范围是（）

A、 $2 < x < 12$ B、 $5 < x < 7$ C、 $1 < x < 6$ D、无法确定

查看试题解析
5. 下列事件属于不可能事件的是（）

A、从装满白球的袋子里随机摸出一个球是白球 B、随时打开电视机，正在播新闻 C、通常情况下，自来水在10℃结冰 D、掷一枚质地均匀的骰子，朝上的一面点数是2

查看试题解析
6. 若 ${(a + 3)}^{2} + \sqrt{b - 2} = 0$ ，则 $a b$ 的值为（）

A、-6 B、6 C、-1 D、1

查看试题解析
7. 下列命题是假命题的是（）

A、对顶角相等 B、两直线平行，内错角相等 C、同位角相等 D、直角三角形两锐角互余

查看试题解析
8. 已知△ABC ，两个完全一样的三角板如图摆放，它们的一组对应直角边分别在AB ， AC上，且这组对应边所对的顶点重合于点M ，点M一定在（）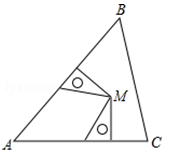

A、∠A的平分线上 B、AC边的高上 C、BC边的垂直平分线上 D、AB边的中线上

查看试题解析

二、填空题

9. 若 $\frac{1}{2 x - 4}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
10. $\sqrt{16}$ 的平方根是．

查看试题解析
11. 如图所示的网格是正方形网格，点A、B、C、D均在格点上，则∠CAB+∠CBA=°．

查看试题解析
12. 计算 $x \div \frac{x}{y} \cdot \frac{1}{x}$ = ．

查看试题解析
13. 请你写出一个比3大且比4小的无理数，该无理数可以是：．

查看试题解析
14. 如图，在Rt△ABC中，∠C=90°，D为BC上一点，连接AD，过D点作DE⊥AB，且DE=DC．若AB=5，AC=3，则EB= ．

查看试题解析
15. 等腰三角形的一个角是70°，则它的顶角的度数是．

查看试题解析
16. 在△ABC中，按以下步骤作图：
①分别以A，C为圆心，以大于 $\frac{1}{2} A C$ 的同样长为半径画弧，两弧相交于两点M，N；

②作直线MN交AB于点D，连结CD．

请回答：若BC=DC，∠B=100°，则∠ACB的度数为．

查看试题解析

三、解答题

17. 计算： $\sqrt{12} + {(3.14 - π)}^{0} - \sqrt[3]{8} + | \sqrt{3} - 2 |$

查看试题解析
18. 计算： $\sqrt{32} \times \sqrt{2} + {(\sqrt{3} - 1)}^{2}$

查看试题解析
19. 计算： $(1 + \frac{1}{a - 1}) \div \frac{a}{a^{2} - 2 a + 1}$

查看试题解析
20. 解分式方程： $\frac{x - 3}{x - 2}$ +1= $\frac{3}{2 - x}$

查看试题解析
21. 如图，BC⊥AD于C，EF⊥AD于F，AB∥DE，分别交BC于B，交EF于E，且BC=EF．求证：AF=CD．

查看试题解析
22. 甲、乙两种机器人都被用来搬运化工原料，甲型机器人比乙型机器人每小时多搬运30千克，甲型机器人搬运900千克所用时间与乙型机器人搬运600千克所用时间相等，两种机器人每小时分别搬运多少化工原料？

查看试题解析
23. 先化简，再代入求值： $\frac{x - 2}{x^{2} + 2 x} \div \frac{x^{2} - 4 x + 4}{x^{2} - 4} - \frac{2}{x}$ ，其中 $x = \sqrt{3}$ ．

查看试题解析
24. 如图：AB=AC，AD⊥BC于D，AE=DE．
求证：

(1)、DE∥AB；

(2)、若∠B=60°，DE=2，求AD的长．

查看试题解析
25. 阅读下列材料，并回答问题：
我们把单位“1”平均分成若干份，表示其中一份的数叫“单位分数”．单位分数又叫埃及分数，在很早以前，埃及人就研究如何把一个单位分数表示成两个或几个单位分数的和或差．今天我们来研究如何拆分一个单位分数．请观察下列各式：

$\frac{1}{6} = \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ； $\frac{1}{12} = \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，

$\frac{1}{20} = \frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$ ， $\frac{1}{30} = \frac{1}{5 \times 6} = \frac{1}{5} - \frac{1}{6}$ ．

(1)、由此可推测 $\frac{1}{56} =$ ；

(2)、请用简便方法计算： $\frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \frac{1}{30} + \frac{1}{42}$ ；

(3)、请你猜想出拆分一个单位分数的一般规律，并用含字母 $m$ 的等式表示出来（ $m$ 表示正整数）；

(4)、仔细观察下面的式子，并用（3）中的规律计算：
$\frac{1}{(x - 2) (x - 3)} - \frac{2}{(x - 1) (x - 3)} + \frac{1}{(x - 1) (x - 2)}$

查看试题解析
26. 已知：在△ABC中，∠ABC=90°，AB=BC，CD平分∠ACB，交AB于D，过B作BE⊥AC交AC于点E，交CD于点F．

(1)、根据描述补全图形；

(2)、试判断△BDF的形状，并说明理由；

(3)、求证： $B E = \frac{1}{2} (B C + B F)$ ．

查看试题解析