北京市房山区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-03-12 类型:期末考试
一、单选题
-
1. 若代数式 有意义,则实数 的取值范围是( )A、 B、 C、 D、2. 下列事件为必然事件的是( )A、打雷后会下雨 B、明天是晴天 C、哥哥的年龄比弟弟的年龄大 D、下雨后会有彩虹3. 下面这四个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 小芳有一串形状、大小差不多的钥匙,其中只有2把能开教室门锁,其余5把是开其他门锁的.在看不见的情况下随意摸出一把钥匙开门锁,小芳能打开教室门锁的可能性为( )A、 B、 C、 D、5. 计算 ,结果正确的是( )A、 B、 C、 D、6. 化简 ,结果正确的是( )A、1 B、-1 C、0 D、±17. 如图,在△ABC中,∠A=45°,∠C=75°,BD是△ABC的角平分线,则∠BDC的度数为( )
4. 小芳有一串形状、大小差不多的钥匙,其中只有2把能开教室门锁,其余5把是开其他门锁的.在看不见的情况下随意摸出一把钥匙开门锁,小芳能打开教室门锁的可能性为( )A、 B、 C、 D、5. 计算 ,结果正确的是( )A、 B、 C、 D、6. 化简 ,结果正确的是( )A、1 B、-1 C、0 D、±17. 如图,在△ABC中,∠A=45°,∠C=75°,BD是△ABC的角平分线,则∠BDC的度数为( ) A、60° B、70° C、75° D、105°8. 如图,在 中, 于 , 于 , 与 交于点 .请你添加一个适当的条件,使 ≌ .下列添加的条件错误的是( )
A、60° B、70° C、75° D、105°8. 如图,在 中, 于 , 于 , 与 交于点 .请你添加一个适当的条件,使 ≌ .下列添加的条件错误的是( )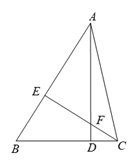 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若分式 的值等于0,则 的值为 .10. 计算: × = .11. 如图是一个可以转动的转盘.盘面上有6个全等的扇形区域,其中1个是红色,2个是绿色,3个是黄色.用力转动转盘,当转盘停止后,指针对准颜色区域的可能性最小,对准颜色区域的可能性最大.
 12. 我国古代数学著作《九章算术》有一个问题:一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处,1丈=10尺,那么折断处离地面的高度是尺.
12. 我国古代数学著作《九章算术》有一个问题:一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处,1丈=10尺,那么折断处离地面的高度是尺.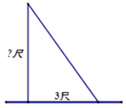 13. 任意掷一枚骰子,面朝上的点数大于2的可能性是 .14. 某校要建立两个计算机教室,为此要购买相同数量的A型计算机和B型计算机.已知一台A型计算机的售价比一台B型计算机的售价便宜400元,如果购买A型计算机需要224 000元,购买B型计算机需要240 000元.求一台A型计算机和一台B型计算机的售价分别是多少元. 设一台B型计算机的售价是x元,依题意列方程为 .15. 已知:如图, ABC中,∠ACB=90°,AC=BC= , ABD是等边三角形,则CD的长度为 .
13. 任意掷一枚骰子,面朝上的点数大于2的可能性是 .14. 某校要建立两个计算机教室,为此要购买相同数量的A型计算机和B型计算机.已知一台A型计算机的售价比一台B型计算机的售价便宜400元,如果购买A型计算机需要224 000元,购买B型计算机需要240 000元.求一台A型计算机和一台B型计算机的售价分别是多少元. 设一台B型计算机的售价是x元,依题意列方程为 .15. 已知:如图, ABC中,∠ACB=90°,AC=BC= , ABD是等边三角形,则CD的长度为 . 16. 如图,长方形ABCD中,AB=6,BC=2,直线l是长方形ABCD的一条对称轴,且分别与AD,BC交于点E,F,若直线l上的动点P,使得△PAB和△PBC均为等腰三角形.则动点P的个数有个.
16. 如图,长方形ABCD中,AB=6,BC=2,直线l是长方形ABCD的一条对称轴,且分别与AD,BC交于点E,F,若直线l上的动点P,使得△PAB和△PBC均为等腰三角形.则动点P的个数有个.
三、解答题
-
17. 计算:(1)、(2)、18. 已知:如图,点B,F,C,E在一条直线上,AB=DE,AC=DF,BF=EC.求证: ABC≌ DEF.
 19. 解方程: ﹣ =1.20. 已知: ABC.求作:射线BM,使它平分∠ABC,交AC于点M.(保留作图痕迹,不要求写作法,指明结果)
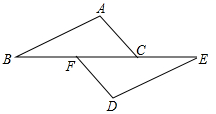
19. 解方程: ﹣ =1.20. 已知: ABC.求作:射线BM,使它平分∠ABC,交AC于点M.(保留作图痕迹,不要求写作法,指明结果) 21. 已知:如图,点 , , 在同一直线上, , , .求证: .
21. 已知:如图,点 , , 在同一直线上, , , .求证: . 22. 先化简,再求值: ,其中 .23. 口袋里有除颜色外都相同的4个球,其中有红球、白球和蓝球. 甲乙两名同学玩摸球游戏.规定:无论谁从口袋里随意摸出一个球,摸到红球,算甲赢;摸到白球,算乙赢;摸到蓝球,不分输赢.每一次摸球,根据球的颜色决定输赢后,将球放回口袋里搅匀后下次再摸球.设计下列游戏:(1)、要使甲、乙两人赢的可能性相等,口袋里应放红球、白球和蓝球各多少个?(2)、要使甲赢的可能性比乙赢的可能性大,口袋里应放红球、白球和蓝球各多少个?24. 如图,在 ABC中,AB=AC,∠A=40°,AB的垂直平分线交AC于点D,交AB于点E,连接BD.
22. 先化简,再求值: ,其中 .23. 口袋里有除颜色外都相同的4个球,其中有红球、白球和蓝球. 甲乙两名同学玩摸球游戏.规定:无论谁从口袋里随意摸出一个球,摸到红球,算甲赢;摸到白球,算乙赢;摸到蓝球,不分输赢.每一次摸球,根据球的颜色决定输赢后,将球放回口袋里搅匀后下次再摸球.设计下列游戏:(1)、要使甲、乙两人赢的可能性相等,口袋里应放红球、白球和蓝球各多少个?(2)、要使甲赢的可能性比乙赢的可能性大,口袋里应放红球、白球和蓝球各多少个?24. 如图,在 ABC中,AB=AC,∠A=40°,AB的垂直平分线交AC于点D,交AB于点E,连接BD. (1)、依题意补全图形;(2)、求∠DBC的度数.
(1)、依题意补全图形;(2)、求∠DBC的度数.



