2016年广西百色市中考数学试卷

试卷更新日期：2016-07-20 类型：中考真卷

进入出卷网下载

一、选择题

1. 三角形的内角和等于（　　）

A、90° B、180° C、300° D、360°

查看试题解析
2. 计算：2³=（　　）

A、5 B、6 C、8 D、9

查看试题解析
3.
如图，直线a、b被直线c所截，下列条件能使a∥b的是（　　）

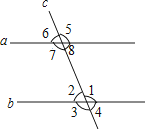A、∠1=∠6 B、∠2=∠6 C、∠1=∠3 D、∠5=∠7

查看试题解析
4. 在不透明口袋内有形状、大小、质地完全一样的5个小球，其中红球3个，白球2个，随机抽取一个小球是红球的概率是（　　）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{3}{5}$ D、 $\frac{2}{5}$

查看试题解析
5. 今年百色市九年级参加中考人数约有38900人，数据38900用科学记数法表示为（　　）

A、3.89×10² B、389×10² C、3.89×10⁴ D、3.89×10⁵

查看试题解析
6.
如图，△ABC中，∠C=90°，∠A=30°，AB=12，则BC=（　　）

A、6 B、6 $\sqrt{2}$ C、6 $\sqrt{3}$ D、12

查看试题解析
7. 分解因式：16﹣x²=（　　）

A、（4﹣x）（4+x） B、（x﹣4）（x+4） C、（8+x）（8﹣x） D、（4﹣x）²

查看试题解析
8. 下列关系式正确的是（　　）

A、35.5°=35°5′ B、35.5°=35°50′ C、35.5°＜35°5′ D、35.5°＞35°5′

查看试题解析
9. 为了了解某班同学一周的课外阅读量，任选班上15名同学进行调查，统计如表，则下列说法错误的是（　　）
阅读量（单位：本/周）
0
1
2
3
4
人数（单位：人）
1
4
6
2
2

A、中位数是2 B、平均数是2 C、众数是2 D、极差是2

查看试题解析
10. 直线y=kx+3经过点A（2，1），则不等式kx+3≥0的解集是（　　）

A、x≤3 B、x≥3 C、x≥﹣3 D、x≤0

查看试题解析
11. A、B两地相距160千米，甲车和乙车的平均速度之比为4：5，两车同时从A地出发到B地，乙车比甲车早到30分钟，若求甲车的平均速度，设甲车平均速度为4x千米/小时，则所列方程是（　　）

A、 $\frac{160}{4 x}$ ﹣ $\frac{160}{5 x}$ =30 B、 $\frac{160}{4 x}$ ﹣ $\frac{160}{5 x}$ = $\frac{1}{2}$ C、 $\frac{160}{5 x}$ ﹣ $\frac{160}{4 x}$ = $\frac{1}{2}$ D、 $\frac{160}{4 x}$ + $\frac{160}{5 x}$ =30

查看试题解析
12.
如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值是（　　）

A、4 B、3 $\sqrt{2}$ C、2 $\sqrt{3}$ D、2+ $\sqrt{3}$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

13. $\frac{1}{3}$ 的倒数是

查看试题解析
14. 若点A（x，2）在第二象限，则x的取值范围是

查看试题解析
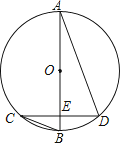
15.
如图，⊙O的直径AB过弦CD的中点E，若∠C=25°，则∠D=

查看试题解析
16.
某几何体的三视图如图所示，则组成该几何体的小正方体的个数是

查看试题解析
17. 一组数据2，4，a，7，7的平均数 $\bar{x}$ =5，则方差S²=

查看试题解析
18. 观察下列各式的规律：
（a﹣b）（a+b）=a²﹣b²
（a﹣b）（a²+ab+b²）=a³﹣b³
（a﹣b）（a³+a²b+ab²+b³）=a⁴﹣b⁴
…
可得到（a﹣b）（a²⁰¹⁶+a²⁰¹⁵b+…+ab²⁰¹⁵+b²⁰¹⁶）=

查看试题解析

三、解答题（本大题共8小题，共66分）

19. 计算： $\sqrt{9}$ +2sin60°+|3﹣ $\sqrt{3}$ |﹣（ $\sqrt{2016}$ ﹣π）⁰ ．

查看试题解析
20. 解方程组： ${\begin{cases} 3 x - y = 2 \\ 9 x + 8 y = 17 \end{cases}$ ．

查看试题解析
21.
△ABC的顶点坐标为A（﹣2，3）、B（﹣3，1）、C（﹣1，2），以坐标原点O为旋转中心，顺时针旋转90°，得到△A′B′C′，点B′、C′分别是点B、C的对应点．

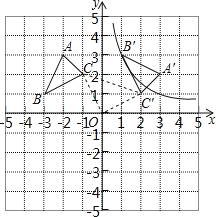(1)、求过点B′的反比例函数解析式；

(2)、求线段CC′的长．

查看试题解析
22.
已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．

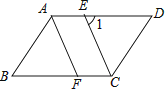(1)、求证：△ABF≌△CDE；

(2)、如图，若∠1=65°，求∠B的大小．

查看试题解析
23.
某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示：
组号
分组
频数
一
6≤m＜7
2
二
7≤m＜8
7
三
8≤m＜9
a
四
9≤m≤10
2

(1)、求a的值；

(2)、若用扇形图来描述，求分数在8≤m＜9内所对应的扇形图的圆心角大小；

(3)、将在第一组内的两名选手记为：A₁、A₂ ，在第四组内的两名选手记为：B₁、B₂ ，从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．

查看试题解析
24.
在直角墙角AOB（OA⊥OB，且OA、OB长度不限）中，要砌20m长的墙，与直角墙角AOB围成地面为矩形的储仓，且地面矩形AOBC的面积为96m² ．

(1)、求这地面矩形的长；

(2)、有规格为0.80×0.80和1.00×1.00（单位：m）的地板砖单价分别为55元/块和80元/块，若只选其中一种地板砖都恰好能铺满储仓的矩形地面（不计缝隙），用哪一种规格的地板砖费用较少？

查看试题解析
25.
如图，已知AB为⊙O的直径，AC为⊙O的切线，OC交⊙O于点D，BD的延长线交AC于点E．

(1)、求证：∠1=∠CAD；

(2)、若AE=EC=2，求⊙O的半径．

查看试题解析
26.
正方形OABC的边长为4，对角线相交于点P，抛物线L经过O、P、A三点，点E是正方形内的抛物线上的动点．

(1)、建立适当的平面直角坐标系，
①直接写出O、P、A三点坐标；
②求抛物线L的解析式；

(2)、求△OAE与△OCE面积之和的最大值．

查看试题解析

阅读量（单位：本/周）	0	1	2	3	4
人数（单位：人）	1	4	6	2	2

组号	分组	频数
一	6≤m＜7	2
二	7≤m＜8	7
三	8≤m＜9	a
四	9≤m≤10	2