2016年广东省深圳市中考数学试卷

试卷更新日期：2016-07-20 类型：中考真卷

进入出卷网下载

一、单项选择题

1. 下列四个数中，最小的正数是（）

A、﹣1 B、0 C、1 D、2

查看试题解析
2.
把下列图标折成一个正方体的盒子，折好后与“中”相对的字是（）

A、祝 B、你 C、顺 D、利

查看试题解析
3. 下列运算正确的是（）

A、8a﹣a=8 B、（﹣a）⁴=a⁴ C、a³•a²=a⁶ D、（a﹣b）²=a²﹣b²

查看试题解析
4. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 据统计，从2005年到2015年中国累积节能1570000000吨标准煤，1570000000这个数用科学记数法表示为（）

A、0.157×10¹⁰ B、1.57×10⁸ C、1.57×10⁹ D、15.7×10⁸

查看试题解析
6.
如图，已知a∥b，直角三角板的直角顶角在直线b上，若∠1=60°，则下列结论错误的是（）

A、∠2=60° B、∠3=60° C、∠4=120° D、∠5=40°

查看试题解析
7. 数学老师将全班分成7个小组开展小组合作学习，采用随机抽签确定一个小组进行展示活动，则第3个小组被抽到的概率是（）

A、 $\frac{1}{7}$ B、 $\frac{1}{3}$ C、 $\frac{1}{21}$ D、 $\frac{1}{10}$

查看试题解析
8. 下列命题正确的是（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、两边及其一角相等的两个三角形全等 C、16的平方根是4 D、一组数据2，0，1，6，6的中位数和众数分别是2和6

查看试题解析
9. 施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x米，则根据题意所列方程正确的是（）

A、 $\frac{2000}{x}$ ﹣ $\frac{2000}{x + 50}$ =2 B、 $\frac{2000}{x + 50}$ ﹣ $\frac{2000}{x}$ =2 C、 $\frac{2000}{x}$ ﹣ $\frac{2000}{x - 50}$ =2 D、 $\frac{2000}{x - 50}$ ﹣ $\frac{2000}{x}$ =2

查看试题解析
10. 给出一种运算：对于函数y=xⁿ ，规定y′=nxⁿ^﹣¹ ．例如：若函数y=x⁴ ，则有y′=4x³ ．已知函数y=x³ ，则方程y′=12的解是（）

A、x₁=4，x₂=﹣4 B、x₁=2，x₂=﹣2 C、x₁=x₂=0 D、x₁=2 $\sqrt{3}$ ，x₂=﹣2 $\sqrt{3}$

查看试题解析
11.
如图，在扇形AOB中∠AOB=90°，正方形CDEF的顶点C是 $\overset{\land}{A B}$ 的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2 $\sqrt{2}$ 时，则阴影部分的面积为（）

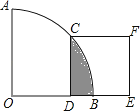A、2π﹣4 B、4π﹣8 C、2π﹣8 D、4π﹣4

查看试题解析
12.
如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：
①AC=FG；②S_△_FAB：S_四边形_CBFG=1：2；③∠ABC=∠ABF；④AD²=FQ•AC，
其中正确的结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 分解因式：a²b+2ab²+b³=

查看试题解析
14. 已知一组数据x₁ ， x₂ ， x₃ ， x₄的平均数是5，则数据x₁+3，x₂+3，x₃+3，x₄+3的平均数是

查看试题解析
15.
如图，在▱ABCD中，AB=3，BC=5，以点B为圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于 $\frac{1}{2}$ PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为

查看试题解析
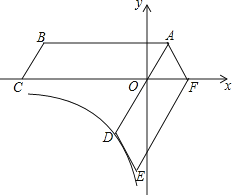
16.
如图，四边形ABCO是平行四边形，OA=2，AB=6，点C在x轴的负半轴上，将▱ABCO绕点A逆时针旋转得到▱ADEF，AD经过点O，点F恰好落在x轴的正半轴上，若点D在反比例函数y= $\frac{k}{x}$ （x＜0）的图象上，则k的值为

查看试题解析

三、解答题：

17. 计算：|﹣2|﹣2cos60°+（ $\frac{1}{6}$ ）^﹣¹﹣（π﹣ $\sqrt{3}$ ）⁰ ．

查看试题解析
18. 解不等式组： ${\begin{cases} 5 x - 1 < 3 (x + 1) \\ \frac{2 x - 1}{3} - 1 \leq \frac{5 x + 1}{2} \end{cases}$ ．

查看试题解析
19.
深圳市政府计划投资1.4万亿元实施东进战略．为了解深圳市民对东进战略的关注情况．某校数学兴趣小组随机采访部分深圳市民，对采访情况制作了统计图表的一部分如下：
关注情况
频数
频率
A．高度关注
M
0.1
B．一般关注
100
0.5
C．不关注
30
N
D．不知道
50
0.25

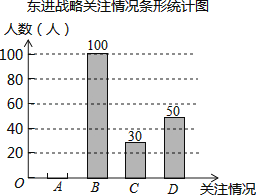(1)、根据上述统计图可得此次采访的人数为人，m= ， n=

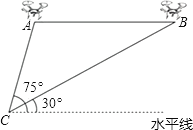
(2)、根据以上信息补全条形统计图；

(3)、根据上述采访结果，请估计在15000名深圳市民中，高度关注东进战略的深圳市民约有人．

查看试题解析
20.
某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）

查看试题解析
21. 荔枝是深圳的特色水果，小明的妈妈先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了1千克桂味和2千克糯米糍，共花费55元．（每次两种荔枝的售价都不变）

(1)、求桂味和糯米糍的售价分别是每千克多少元；

(2)、如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．

查看试题解析
22.
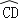如图，已知⊙O的半径为2，AB为直径，CD为弦．AB与CD交于点M，将沿CD翻折后，点A与圆心O重合，延长OA至P，使AP=OA，连接PC．

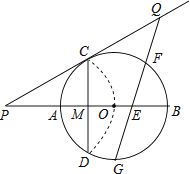(1)、求CD的长；

(2)、求证：PC是⊙O的切线；

(3)、
点G为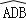的中点，在PC延长线上有一动点Q，连接QG交AB于点E．交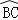于点F（F与B、C不重合）．问GE•GF是否为定值？如果是，求出该定值；如果不是，请说明理由．

查看试题解析
23.
如图，抛物线y=ax²+2x﹣3与x轴交于A、B两点，且B（1，0）

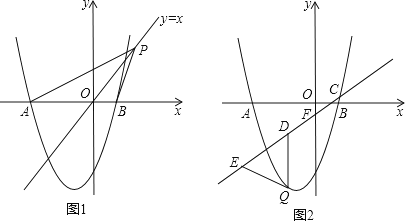(1)、求抛物线的解析式和点A的坐标；

(2)、如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；

(3)、如图2，已知直线y= $\frac{2}{3}$ x﹣ $\frac{4}{9}$ 分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

查看试题解析

关注情况	频数	频率
A．高度关注	M	0.1
B．一般关注	100	0.5
C．不关注	30	N
D．不知道	50	0.25