初中数学苏科版七年级下册 10.4 三元一次方程组同步训练

试卷更新日期：2021-03-11 类型：同步测试

进入出卷网下载

一、单选题

1. 下列方程组中，是三元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 0 \\ y + z = 1 \\ z + w = 5 \end{array}$ B、 ${\begin{array}{l} x + y = 0 \\ y + 2 x = 1 \end{array}$ C、 ${\begin{array}{l} 3 x + 4 z = 7 \\ 2 x + 3 y = 9 - z \\ 5 x - 9 y + 7 z = 8 \end{array}$ D、 ${\begin{array}{l} x^{2} - 2 y = 0 \\ y + z = 3 \\ x + y + z = 1 \end{array}$

查看试题解析
2. 方程组 ${\begin{cases} x + y = - 1 \\ x + z = 0 \\ y + z = 1 \end{cases}$ 的解是（）

A、 ${\begin{cases} x = - 1 \\ y = 1 \\ z = 0 \end{cases}$ B、 ${\begin{cases} x = 1 \\ y = 0 \\ z = - 1 \end{cases}$ C、 ${\begin{cases} x = 0 \\ y = 1 \\ z = - 1 \end{cases}$ D、 ${\begin{cases} x = - 1 \\ y = 0 \\ z = 1 \end{cases}$

查看试题解析
3. 已知 ${\begin{cases} x = 1 \\ y = 2 \\ z = 3 \end{cases}$ 是方程组 ${\begin{cases} a x + b y = 2 \\ b y + c z = 3 \\ c x + a z = 7 \end{cases}$ 的解，则a+b+c的值是（）

A、3 B、2 C、1 D、无法确定

查看试题解析
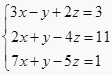4. 解方程组，若要使计算简便，消元的方法应选取（）

A、先消去x B、先消去y C、先消去z D、以上说法都不对

查看试题解析
5. 将三元一次方程组 ${\begin{matrix} 5 x + 4 y + z = 0 ① \\ 3 x + y - 4 z = 11 ② \\ x + y + z = - 2 ③ \end{matrix}$ ，经过①-③和③×4+②消去未知数z后，得到的二元一次方程组是（）

A、 ${\begin{matrix} 4 x + 3 y = 2 \\ 7 x + 5 y = 3 \end{matrix}$ B、 ${\begin{matrix} 4 x + 3 y = 2 \\ 23 x + 17 y = 11 \end{matrix}$ C、 ${\begin{matrix} 3 x + 4 y = 2 \\ 23 x + 17 y = 11 \end{matrix}$ D、 ${\begin{matrix} 3 x + 4 y = 2 \\ 7 x + 5 y = 3 \end{matrix}$

查看试题解析
6. 若三元一次方程组 ${\begin{matrix} x + y = 5 \\ x + z = - 1 \\ y + z = - 2 \end{matrix}$ 的解使ax+2y+z=0，则a的值为（）

A、1 B、0 C、﹣2 D、4

查看试题解析
7. 方程组 ${\begin{cases} a - b + c = 0 \\ 4 a + 2 b + c = 3 \\ 25 a + 5 b + c = 60 \end{cases}$ 消去字母c后，得到的方程一定不是（　　）

A、a+b＝1 B、a﹣b＝1 C、4a+b＝10 D、7a+b＝19

查看试题解析
8. 有甲、乙、丙三种商品，如果购甲3件，乙2件，丙1件共需315元钱，购甲1件，乙2件，丙3件共需285元钱，那么购甲、乙、丙三种商品各一件共需（）

A、50元 B、100元 C、150元 D、200元

查看试题解析
9. 如图，“ $●$ 、 $■$ 、 $▲$ ”分别表示三种不同的物体 $.$ 已知前两架天平保持平衡，要使第三架也保持平衡 $.$ 如果在“？”处只放“ $■$ ”，那么应放“ $■$ ” $($ $)$

A、3个 B、4个 C、5个 D、6个

查看试题解析
10. 如图，在某张桌子上放相同的木块，R=34，S=92，则桌子的高度是（）

A、63 B、58 C、60 D、55

查看试题解析

二、填空题

11. 已知 ${\begin{matrix} x + y = 5 \\ y + z = - 2 \\ z + x = 3 \end{matrix}$ ，则x＋y＋z＝.

查看试题解析
12. 设 ${\begin{array}{l} 2 x + y + 3 z = 23 \\ x + 4 y + 5 z = 36 \end{array}$ ，则3x-2y+z= ．

查看试题解析
13. 已知等式y＝ax²＋bx＋c，a≠0，当x＝-3时，y＝0；当x＝4时，y＝0，则关于x的式子a (x-1)²＝-4b-c中x的值为.

查看试题解析
14. 若 $4 x - 3 y - 6 z = 0$ ， $x + 2 y - 7 z = 0 (x y z \neq 0)$ ，则代数式 $\frac{5 x^{2} + 2 y^{2} - z^{2}}{2 x^{2} - 3 y^{2} - 10 z^{2}}$ 的值是.

查看试题解析
15. 为确保信息安全，信息需加密传输，发送方由明文→密文（加密）；接收方由密文→明文（解密）．已知加密规则为：明文a，b，c，d对应的密文为a+b，b+c，c+d，d+2a．例如：明文1，2，3，4对应的密文为3，5，7，6．当接收方收到密文8，11，15，15时，则解密得到的明文应为．

查看试题解析
16. 一次数学竞赛准备了22 支铅笔作为奖品发给一、二、三等奖的学生,原计划发给一等奖每人6支,二等奖每人3 支,三等奖每人2支,后来改为一等奖每人9支,二等奖每人4支,三等奖每人1支,则获一、二等奖的学生总共有人.

查看试题解析
17. 由不同生产商提供 $10$ 套校服参加比选，甲、乙、两三个同学分别参加比选，比选后结果是：每套校服至少有一人选中，且每人都选中了其中的 $6$ 套校服．如果将其中只有 $1$ 人选中的校服称作“不受欢迎校服”， $2$ 人选中的校服称作“颇受欢迎校服”， $3$ 人都选中的校服称作“最受欢迎校服”，则“不受欢迎校服”比“最受欢迎校服”多套．

查看试题解析
18. 某单位招聘员工采取笔试与面试相结合的方式进行，两项成绩满分均为100分．根据规定，笔试成绩和面试成绩分别按一定的百分比折合综合成绩（综合成绩的满分仍为100分）．已知小明应聘的笔试成绩为85分，面试成绩为90分，现得知小明的最后综合成绩为88分．设小明的笔试成绩所占的百分比为x，面试成绩所占的百分比为y，根据题意列方程组得

查看试题解析

三、解答题

19. 解三元一次方程组：

(1)、 ${\begin{matrix} 3 x - y + z = 4 \\ 2 x + 3 y - z = 12 \\ x + y + z = 6 \end{matrix}$

(2)、 ${\begin{matrix} x + z - 3 = 0 \\ 2 x - y + 2 z = 2 \\ x - y - z = - 3 \end{matrix}$ ．

查看试题解析
20. 在等式y＝ax²+bx+c中，当x＝﹣1时，y＝3；当x＝0时，y＝1，当x＝1时，y＝1，求这个等式中a、b、c的值.

查看试题解析
21. 若a，b，c表示三角形的三边，此三角形的周长是18，且a+b=2c，b=2a，求三边长.

查看试题解析
22. 有三个数，第一个数的3倍比第二个数的5倍小90，而第一个数的4倍与第二个数的6倍之差等于第三个数的20倍的相反数，同时，第三个数比4大1．求这三个数．

查看试题解析
23. 一个三位数，如果把它的个位数字与百位数字交换位置，那么所得的新数比原数小99，且各位数字之和为14，十位数字是个位数字与百位数字之和．求这个三位数．

查看试题解析
24. 某学校计划用104 000元购置一批电脑（这批款项须恰好用完，不得剩余或追加）．经过招标，其中平板电脑每台1600元，台式电脑每台4000元，笔记本电脑每台4600元．
（1）若学校同时购进其中两种不同类型的电脑共50台，请你帮学校设计该如何购买；
（2）若学校同时购进三种不同类型的电脑共26台（三种类型的电脑都有），并且要求笔记本电脑的购买量不少于15台，请你帮学校设计购买方案．

查看试题解析
25. 2013年4月20日8时2分在四川省雅安市芦山县发生7.0级地震，有1.8万人等待安置，各地人民纷纷捐款灾区．某市一企业在得知灾区急需帐篷后立即与厂家联系购买帐篷送往灾区．已知用9万元刚好可以从厂家购进帐篷500顶．该厂家生产三种不同规格的帐篷，出厂价分别为甲种帐篷每顶150元，乙种帐篷每顶210元，丙种帐篷每顶250元．
①若企业同时购进其中两种不同规格的帐篷，则企业的购买方案有哪几种？
②若企业想同时购进三种不同规格的帐篷，必须每种帐篷都有，为了便于分类打包，每种帐篷数都要求是10的倍数．请你研究一下是否可行？如果可行请给出符合条件的设计方案；若不可行，请说明理由．

查看试题解析
26. 有一场足球比赛，共有九支球队参加，采取单循环赛，其记分和奖励方案如下表：

标准

胜一场

平一场

负一场

积分

3

1

0

奖励（元／人）

2000

800

0

甲队参加完了全部8场比赛，共得积分16分．

(1)、求甲队胜负的所有可能情况；

(2)、若每一场比赛，每一个参赛队员均可得出场费500元，求甲队参加了所有8场比赛的队员的个人总收入（奖金加上出场费）．

查看试题解析
27. 解二元一次方程组的关键是“消元”，即把“二元”转化为“一元”，同样，我们可以用“消元”的方法解三元一次方程组．下面，我们就来解一个三元一次方程组：
解方程组 ${\begin{array}{l} x + y + z = 2 ， ① \\ 2 x + 3 y - z = 8 ， ② \\ 3 x - 2 y + z = 3 ， ③ \end{array}$
小曹同学的部分解答过程如下：
解：______+______，得3x+4y=10，④
______+______，得5x+y=11，⑤
______与______联立，得方程组
${\begin{array}{l} 3 x + 4 y = 10 \\ 5 x + y = 11 \end{array}$

(1)、请你在方框中补全小曹同学的解答过程：

(2)、若m、n、p、q满足方程组 ${\begin{array}{l} m + n + p + q = 4 \\ 2 (m + n) + 3 p - q = 16 \\ 3 (m + n) - 2 p + q = 6 \end{array}$ ，则m+n-2p+q= ．

查看试题解析
28. 某商场计划用56000元从厂家购进60台新型电子产品，已知该厂家生产甲乙、丙三种不同型号的电子产品，设甲、乙型设备应各买入x，y台，其中每台的价格、销售获利如下表：

甲型

乙型

丙型

价格(元/台)

1000

800

500

销售获利(元/台)

260

190

120

(1)、购买丙型设备台(用含x，y的代数式表示)；

(2)、若商场同时购进三种不同型号的电子产品(每种型号至少有一台)，恰好用了56000元，则商场有哪几种购进方案？

(3)、在第(2)题的基础上，为了使销售时获利最多，应选择哪种购进方案？此时获利为多少？

查看试题解析

标准	胜一场	平一场	负一场
积分	3	1	0
奖励（元／人）	2000	800	0

	甲型	乙型	丙型
价格(元/台)	1000	800	500
销售获利(元/台)	260	190	120

初中数学苏科版七年级下册 10.4 三元一次方程组 同步训练

一、单选题

二、填空题

三、解答题

初中数学苏科版七年级下册 10.4 三元一次方程组同步训练