初中数学湘教版八年级下册2.2.1平行四边形的性质 同步练习
试卷更新日期：2021-03-11 类型：同步测试
一、单选题
-
1. 如图，在▱ABCD中，下列说法一定正确的是（ ）
A、AC＝BD B、AC⊥BD C、AB＝CD D、AB＝BC2. 如图，四边形 是平行四边形， 是 延长线上的一点，若 ，则 的度数是（ ）
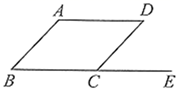A、 B、 C、 D、3. 已知 的周长为32cm，对角线 、 相交于点O，若 的周长比 的周长大4cm，则 的长是（ ）．A、4cm B、6cm C、8cm D、10cm4. 如图，平行四边形ABCD的对角线交于点O，且AB＝8，△OCD的周长为20，则平行四边形ABCD的两条对角线的和是（ ）
A、40 B、28 C、24 D、125. 如图，平行四边形 的对角线 相交于点 ，且 则 的周长是（ ）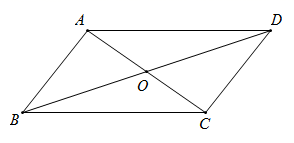
A、 B、 C、 D、6. 平行四边形ABCD中，∠A=50°，则∠B的度数是（ ）A、40° B、50° C、130° D、150°7. 如图，在平行四边形ABCD中，AB=5，BE平分∠ABC交CD边于点E，且DE=2，则BC的长为（ ）
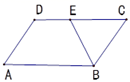A、6 B、5 C、4 D、38. 如图，在▱ABCD中，已知AD＝5cm，AB＝3cm，AE平分∠BAD交BC边于点E，则EC等于（ ）
A、1.5cm B、2cm C、2.5cm D、3cm9. 若平行四边形中两个内角的度数之比为1：2，则其中较小的内角是（ ）A、30° B、45° C、60° D、90°10. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF，CF，则下列结论中不一定成立的是（ ）
A、S△BEC=2S△CEF B、EF=CF C、∠DCF= ∠BCD D、∠DFE=3∠AEF二、填空题
-
11. 在 中，已知 ，它的周长为 .12. 在平行四边形ABCD中，∠B+∠D=200°，则∠A的度数为.13. 如图，将平行四边形 放置在平面直角坐标系 中， 为坐标原点，若点 的坐标是 ，点 的坐标是 ，则点 的坐标是 ．
14. 如图，点O是▱ABCD的对角线交点，AD＞AB，E、F是AB边上的点，且EF= AB；G、H是BC边上的点，且GH= BC，若S1 ， S2分别表示△EOF和△GOH的面积，则S1：S2= ．
三、解答题
-
15. 已知，如图，在平行四边形ABCD中，∠A=135°，AB=5cm，BC=9 cm，求∠B，∠C的大小及AD，CD的长.
16. 如图，在 中，∠ABC的平分线BE交AD于点E，测得∠AEB=27°，求∠D的度数．
