初中数学苏科版七年级下册 9.4 乘法公式同步训练

试卷更新日期：2021-03-10 类型：同步测试

进入出卷网下载

一、单选题

1. 在计算( $x + 2 y$ ) ( $- 2 y + x$ )时，最佳的方法是（）

A、运用多项式乘多项式法则 B、运用平方差公式 C、运用单项式乘多项式法则 D、运用完全平方公式

查看试题解析
2. 下列整式运算正确的是（）

A、（a﹣b）²＝a²﹣b² B、（a+2）（a﹣2）＝a²﹣2 C、（a+2）（a﹣2）＝a²﹣4 D、 ${(a + 2 b)}^{2} = a^{2} + 2 a b + 4 b^{2}$

查看试题解析
3. 若 $a + b = 100$ ， $a b = 48$ ，那么 $a^{2} + b^{2}$ 值等于（）

A、5200 B、1484 C、5804 D、9904

查看试题解析
4. 如果 $x^{2} + x = 3$ ，那么代数式 $(x + 1) (x - 1) + x (x + 2)$ 的值是（）

A、2 B、3 C、5 D、6

查看试题解析
5. 如果（a+b）²＝16，（a﹣b）²＝4，且a、b是长方形的长和宽，则这个长方形的面积是（）

A、3 B、4 C、5 D、6

查看试题解析
6. 我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图①可以用来解释(a＋b)²－(a－b)²＝4ab.那么通过图②中阴影部分面积的计算验证了一个恒等式，此等式是（）

A、a²－b²＝(a＋b)(a－b) B、(a－b)²＝a²－2ab＋b² C、(a＋b)²＝a²＋2ab＋b² D、(a－b)(a＋2b)＝a²＋ab－b²

查看试题解析
7. 定义新运算：a*b＝ab+a²﹣b² ，则（x+y）*（x﹣y）＝（）

A、x²﹣y² B、x²﹣y²﹣2xy C、x²﹣y²﹣4xy D、x²﹣y²+4xy

查看试题解析
8. 计算（x+1）（x²+1）（x﹣1）的结果正确的是（　　）

A、x⁴+1 B、（x+1）⁴ C、x⁴﹣1 D、（x﹣1）⁴

查看试题解析
9. 已知 $a - b = b - c = \frac{2}{5},$ 且 $a^{2} + b^{2} + c^{2} = 1$ ，则 $a b + b c + a c$ 的值（）

A、 $\frac{13}{25}$ B、 $- \frac{2}{25}$ C、 $\frac{19}{25}$ D、 $\frac{18}{25}$

查看试题解析
10. 如图，有A，B，C三种不同型号的卡片，每种各10张.A型卡片是边长为a的正方形，B型卡片是相邻两边长分别为a、b的长方形，C型卡片是边长为b的正方形.从中取出若干张卡片（每种卡片至少一张），把取出的这些卡片拼成一个正方形，所有符合要求的正方形的个数是（）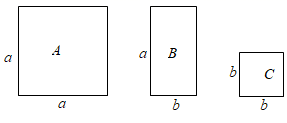

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 计算： $2021 \times 2019 - 2020^{2} =$

查看试题解析
12. 已知 $x=y+4$ ，则代数式 $x^{2} - {2xy+y}^{2} - 25$ 的值为．

查看试题解析
13. 若x²＋2(m－3)x＋16是完全平方式，则m表示的数是.

查看试题解析
14. 若（2a﹣3b）²=（2a+3b）²+N，则表示N的代数式是．

查看试题解析
15. 若x²+4x+8y+y²+20＝0，则x﹣y＝．

查看试题解析
16. 若规定符号 $| \begin{matrix} a & b \\ c & d \end{matrix} |$ 的意义是： $| \begin{matrix} a & b \\ c & d \end{matrix} |$ =ad﹣bc，则当m²﹣2m﹣3=0时， $| \begin{matrix} m^{2} & m - 3 \\ 1 - 2 m & m - 2 \end{matrix} |$ 的值为．

查看试题解析
17. 利用平方差计算（2+1）（2²+1）（2⁴+1）（2⁸+1）+1＝．

查看试题解析
18. 若a=2009x+2007，b=2009x+2008，c=2009x+2009，则a²+b²+c²﹣ab﹣bc﹣ca的值为.

查看试题解析

三、解答题

19. 先化简，再求值：（x+y+2）（x+y﹣2）﹣（x+2y）²+3y² ，其中x=﹣ $\frac{1}{2}$ ，y= $\frac{1}{3}$ ．

查看试题解析
20. 先化简，再求值：(x＋y)²－2x(x＋3y)＋(x＋2y)(x－2y)，其中x＝－1，y＝2．

查看试题解析
21. 若|x﹣y+1|与（x+2y+4）²互为相反数，化简求代数[（2x+2y）²﹣（3x+y）（3x﹣y）﹣5y²]÷（2x）的值．

查看试题解析
22. 小明同学在学习整式时发现，如果合理地使用乘法公式可以简化运算，于是在解此道计算题时他是这样做的（如下）：
${(2 x - 3 y)}^{2} - (x - 2 y) (x + 2 y)$

$= 4 x^{2} - 6 x y + 3 y^{2} - x^{2} - 2 y^{2}$ 第一步

$= 3 x^{2} - 6 x y + y^{2}$ 第二步

小华看到小明的做法后，对他说：“你做错了，在第一步运用公式时出现了错误，你好好检查一下.”小明认真仔细检查后，自己发现了一处错误圈画了出来，并进行了纠正（如下）：

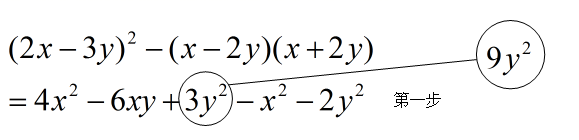
小华看到小明的改错后说：“你还有错没有改出来.”

(1)、你认为小华说的对吗？（填“对”或“不对”）；

(2)、如果小华说的对，那么小明还有哪些错误没有找出来，请你帮助小明把第一步中的其它错误圈画出来并改正，然后写出此题的正确解题过程.

查看试题解析
23. 在边长为a的正方形的一角减去一个边长为 $b$ 的小正方形（ $a > b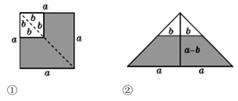$ ），如图①

(1)、由图①得阴影部分的面积为；

(2)、沿图①中的虚线剪开拼成图②，则图②中阴影部分的面积为；

(3)、由（1）（2）的结果得出结论：=；

(4)、利用（3）中得出的结论计算： $2020^{2} - 2019^{2}$

查看试题解析
24.

(1)、已知 $a - b = 2$ ， $a b = 5$ ，求 $a^{2} + b^{2} - 3 a b$ 的值；

(2)、已知 $a^{2} - a - 1 = 0$ ，求 $a^{3} - 2 a^{2} + 3$ 的值．

(3)、如图，有A型、B型、C型三种不同类型的纸板，其中A型是边长为a的正方形，B型是长为a，宽为b的长方形，C型是边长为b的正方形．若想用这些纸板拼成一个长方形，使其面积为 $(a + b) (a + 2 b)$ ．
完成下列各题：

①填空 $(a + b) (a + 2 b)$ =；

②请问需要A型纸板、B型纸板、C型纸板各多少张？试说明理由．

查看试题解析
25. 如图①所示是一个长为 $2 m$ ，宽为 $2 n$ 的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形，根据这一操作过程回答下列问题：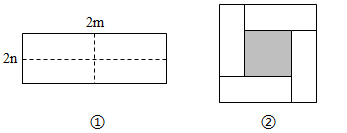

(1)、图②中阴影部分的正方形的边长为；

(2)、请用两种方法表示图②中阴影部分的面积.
方法一：；方法二：；

(3)、观察图②，写出代数式 ${(m + n)}^{2}$ 、 ${(m - n)}^{2}$ 、 $m n$ 之间的等量关系式：；

(4)、计算： ${(10.5 + 2)}^{2} - {(10.5 - 2)}^{2} =$ .

查看试题解析
26. 乘法公式的探究及应用.

(1)、小题1：如图1，可以求出阴影部分的面积是(写成两数平方差的形式)；

(2)、小题2：如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是，长是，面积是(写成多项式乘法的形式).

(3)、小题3：比较图 1，图2的阴影部分面积，可以得到乘法公式 (用式子表达).

查看试题解析
27. 从边长为 a 的正方形剪掉一个边长为 b 的正方形（如图 1），然后将剩余部分拼成一个长方形（如图 2）.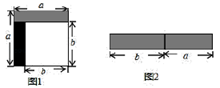

(1)、上述操作能验证的等式是（请选择正确的一个）

A、a $^{2}$ ﹣2ab+b $^{2}$ ＝（a﹣b） $^{2}$ B、a $^{2}$ ﹣b $^{2}$ ＝（a+b）（a﹣b） C、a $^{2}$ +ab＝a（a+b）

(2)、若 x $^{2}$ ﹣9y $^{2}$ ＝12，x+3y＝4，求 x﹣3y 的值；

(3)、计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{2019^{2}}) (1 - \frac{1}{2020^{2}})$ .

查看试题解析
28. 如图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀剪成四块完全一样的小长方形，然后按图2的形状拼成一个正方形。

(1)、图2中的阴影部分的正方形的边长是。

(2)、请用两种不同的方法表示图2中阴影部分的面积，并写出下列三个代数式：(a+b)²，(a-b)²，ab之间的等量关系；

(3)、利用(2)中的结论计算：x-y=2，xy= $\frac{5}{4}$ ，求x+y的值；

(4)、根据(2)中的结论，直接写出m+ $\frac{1}{m}$ 和m- $\frac{1}{m}$ 之间的关系；若m²-4m+1=0，分别求出m+ $\frac{1}{m}$ 和(m- $\frac{1}{m}$ )²的值。

查看试题解析

初中数学苏科版七年级下册 9.4 乘法公式 同步训练

一、单选题

二、填空题

三、解答题

初中数学苏科版七年级下册 9.4 乘法公式同步训练