初中数学苏科版七年级下册 9.4 乘法公式——完全平方公式同步训练

试卷更新日期：2021-03-10 类型：同步测试

进入出卷网下载

一、单选题

1. ${(- a + b)}^{2}$ 等于（）

A、 $a^{2} + b^{2}$ B、 $a^{2} - 2 a b + b^{2}$ C、 $a^{2} - b^{2}$ D、 $a^{2} + 2 a b + b^{2}$

查看试题解析
2. 下列等式能够成立的是（）

A、（2x-y）²=4x²-2xy+y² B、（x+y）²=x²+y² C、（ $\frac{1}{2}$ a-b）²= $\frac{1}{4}$ a²-ab+b² D、（ $\frac{1}{x}$ +x）²= $\frac{1}{x^{2}}$ +x²

查看试题解析
3. 若代数式x²-6x+b可化为(x-a)²-1，则b-a的值是（）

A、5 B、－5 C、11 D、－11

查看试题解析
4. 已知a+b=-5，ab=-4，则a²-ab+b²的值是（　　）

A、37 B、33 C、29 D、21

查看试题解析
5. 已知x﹣y＝3，xy＝1，则x²+y²＝（　　）

A、5 B、7 C、9 D、11

查看试题解析
6. 若 $a - b = 1$ ， $a^{2} + b^{2} = 13$ ，则 $a b$ 的值为（）

A、6 B、7 C、8 D、9

查看试题解析
7. 对于任何实数m、n，多项式m²+n²-6m-10n+36的值总是（）

A、非负数 B、0 C、大于2 D、不小于2

查看试题解析
8. 已知（m $-$ 2018）²+（m $-$ 2020）² $=$ 34，则（m $-$ 2019）²的值为（）

A、4 B、8 C、12 D、16

查看试题解析
9. 小淇将（2019x+2020）²展开后得到a₁x²+b₁x+c₁；小尧将（2020x﹣2019）²展开后得到a₂x²+b₂x+c₂ ，若两人计算过程无误，则c₁﹣c₂的值为（）

A、2019 B、2020 C、4039 D、1

查看试题解析
10. 已知a＝2019x+2018，b＝2019x+2019，c＝2019x+2020．则多项式a²+b²+c²﹣ab﹣bc﹣ac的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 若a+b=17，ab=60，则（a- b）²=

查看试题解析
12. 若a²+b²=6，a+b=3，则ab的值为．

查看试题解析
13. 已知x﹣ $\frac{1}{x}$ ＝6，求x²+ $\frac{1}{x^{2}}$ 的值为.

查看试题解析
14. 已知xy=-3，x+y=-4，则x²-xy+y²的值为．

查看试题解析
15. 计算：2020²﹣4040×2019+2019²＝.

查看试题解析
16. 设(a＋2b)²＝(a－2b)²＋A，则A＝.

查看试题解析
17. 已知 $x + y = 1$ ，则 $\frac{1}{2} x^{2} + x y + \frac{1}{2} y^{2}$ 的值是．

查看试题解析
18. 已知关于 $x$ 的二次三项式 $x^{2} - (a - 1) x + 4$ 是完全平方式，则a=.

查看试题解析
19. 我围古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中，用如图的三角形解释二项和(a+b)“的展开式的各项系数，此三角形称为“杨辉三角”.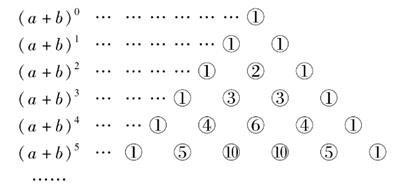

根据“杨辉三角”请计算(a+b)²⁰的展开式中第三项的系数为.

查看试题解析

三、解答题

20. 计算：（a+b+c）²

查看试题解析
21. 先化简，再计算：（2a+b）（b﹣2a）﹣（a﹣3b）² ，其中a=﹣2，b= $\frac{3}{2}$ ．

查看试题解析
22. 已知（x+y）²=25，（x﹣y）²=81，求x²+y²和xy的值．

查看试题解析
23. 已知 $a + b = 6$ ， $a b = 2$ ，求下列各式的值.

(1)、 $a^{2} + b^{2}$ ；

(2)、 ${(a - b)}^{2}$ ；

(3)、 $a^{2} - a b + b^{2}$ .

查看试题解析
24.

(1)、当 $a = 2$ ， $b = \frac{1}{2}$ 时，分别求代数式 $a^{2} - 2 a b + b^{2}$ 和 ${(a - b)}^{2}$ 的值；

(2)、当 $a = - 5$ ， $b = - 3$ 时， $a^{2} - 2 a b + b^{2}$ ${(a - b)}^{2}$ （填“ $=$ ”，“ $<$ ”，“ $>$ ”）

(3)、观察（1）（2）中代探索代数式 $a^{2} - 2 a b + b^{2}$ 和 ${(a - b)}^{2}$ 有何数量关系，并把探索的结果写出来： $a^{2} - 2 a b + b^{2}$ ${(a - b)}^{2}$ （填“ $=$ ”，“ $<$ ”，“ $>$ ”）

(4)、利用你发现的规律，求 ${135.7}^{2} - 2 \times 135.7 \times 35.7 + {35.7}^{2}$ 的值.

查看试题解析
25. 如图1，A纸片是边长为a的正方形，B纸片是边长为b的正方形，C纸片是长为b，宽为a的长方形.现用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形.

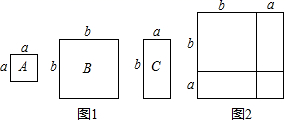(1)、请用两种不同的方法求图2大正方形的面积.
方法1：；方法2：；

(2)、观察图2，请你写出下列三个代数式：（a+b）² ， a²+b² ， ab之间的等量关系；

(3)、根据（2）题中的等量关系，解决如下问题：若a+b=5，a²+b²=13，求ab的值；

查看试题解析
26. （阅读理解）“若 $x$ 满足 $(70 - x) (x - 50) = 30$ ，求 ${(70 - x)}^{2} + {(x - 50)}^{2}$ 的值”.
解：设 $70 - x = a$ ， $x - 50 = b$ ，则 $(70 - x) (x - 50) = a b = 30$ ，
$a + b = (70 - x) + (x - 50) = 20$ ，
${(70 - x)}^{2} + {(x - 50)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 20^{2} - 2 \times 30 = 340$
（解决问题）

(1)、若 $x$ 满足 $(40 - x) (x - 30) = - 20$ ，则 ${(40 - x)}^{2} + {(x - 30)}^{2}$ 的值为；

(2)、若满足 $(2 x - 3) (x - 1) = \frac{9}{4}$ ，则 ${(3 - 2 x)}^{2} + 4 {(x - 1)}^{2}$ 的值为；

(3)、如图，正方形 $A B C D$ 的边长为 $x$ ， $A E = 14$ ， $C G = 30$ ，长方形 $E F G D$ 的面积是200，四边形 $N G D H$ 和 $M E D Q$ 都是正方形，四边形 $P Q D H$ 是长方形，求图中阴影部分的面积（结果必须是一个具体的数值）.

查看试题解析

初中数学苏科版七年级下册 9.4 乘法公式——完全平方公式 同步训练

一、单选题

二、填空题

三、解答题

初中数学苏科版七年级下册 9.4 乘法公式——完全平方公式同步训练