高中数学人教A版(2019)选择性必修第二册5.1.2导数的概念及其几何意义
试卷更新日期:2021-03-09 类型:同步测试
一、单选题
-
1. 函数f(x)在x=x0处的导数可表示为( )A、f′(x0)= B、f′(x0)= C、f′(x0)=f(x0+Δx)-f(x0) D、f′(x0)=2. 已知曲线 在 处的切线方程是 ,则 (5)与 (5)分别为( )A、3,3 B、3,-1 C、-1,3 D、0,-13. 函数 在 处的导数 的几何意义是( )A、在点 处与 的图象只有一个交点的直线的斜率 B、过点 的切线的斜率 C、点 与点 的连线的斜率 D、函数 的图象在点 处的切线的斜率4. 某司机看见前方 处有行人横穿马路,这时司机开始紧急刹车,在刹车的过程中,汽车速度v是关于刹车时间t的函数,其图象可能是( )A、
 B、
B、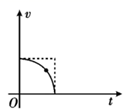 C、
C、 D、
D、 5. 如图,函数的图象在P点处的切线方程是 ,若点 的横坐标是5,则 ( )
5. 如图,函数的图象在P点处的切线方程是 ,若点 的横坐标是5,则 ( ) A、 B、1 C、2 D、06. 已知函数 在 上有导函数, 图象如图所示,则下列不等式正确的是( )
A、 B、1 C、2 D、06. 已知函数 在 上有导函数, 图象如图所示,则下列不等式正确的是( ) A、 B、 C、 D、7. 曲线 在 处的切线平行于直线 ,则 点的坐标为( )A、(1, 0) B、(2, 8) C、(1, 0)和(-1, -4) D、(2, 8)和(-1, -4)8. 若曲线 的一条切线经过点 ,则此切线的斜率为( )A、 B、 C、 或 D、 或9. 函数 在点 处的切线斜率为 ,则 的最小值是( )A、10 B、9 C、8 D、10. 甲、乙两厂污水的排放量W与时间 的关系如图所示,则治污效果较好的是( )
A、 B、 C、 D、7. 曲线 在 处的切线平行于直线 ,则 点的坐标为( )A、(1, 0) B、(2, 8) C、(1, 0)和(-1, -4) D、(2, 8)和(-1, -4)8. 若曲线 的一条切线经过点 ,则此切线的斜率为( )A、 B、 C、 或 D、 或9. 函数 在点 处的切线斜率为 ,则 的最小值是( )A、10 B、9 C、8 D、10. 甲、乙两厂污水的排放量W与时间 的关系如图所示,则治污效果较好的是( ) A、甲厂 B、乙厂 C、两厂一样 D、不确定11. 已知函数 和 在区间 上的图象如图所示,则下列说法正确的是( )
A、甲厂 B、乙厂 C、两厂一样 D、不确定11. 已知函数 和 在区间 上的图象如图所示,则下列说法正确的是( ) A、 在a到b之间的平均变化率大于 在a到b之间的平均变化率 B、 在a到b之间的平均变化率小于 在a到b之间的平均变化率 C、对于任意 ,函数 在 处的瞬时变化率总大于函数 在 处的瞬时变化率 D、存在 ,使得函数 在 处的瞬时变化率小于函数 在 处的瞬时变化率12. 函数 的图象如图所示,则下列数值排序正确的是( )
A、 在a到b之间的平均变化率大于 在a到b之间的平均变化率 B、 在a到b之间的平均变化率小于 在a到b之间的平均变化率 C、对于任意 ,函数 在 处的瞬时变化率总大于函数 在 处的瞬时变化率 D、存在 ,使得函数 在 处的瞬时变化率小于函数 在 处的瞬时变化率12. 函数 的图象如图所示,则下列数值排序正确的是( )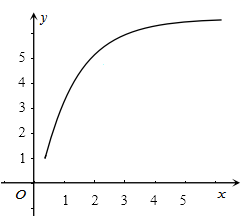 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
13. 已知曲线 在点P处的切线平行于直线 ,那么点P的坐标为( )A、 B、 C、 D、14. 下列命题正确的是( )A、若 ,则函数 在 处无切线 B、函数 的切线与函数的图象可以有两个公共点 C、曲线 在 处的切线方程为 ,则当 时, D、若函数 的导数 ,且 ,则 的图象在 处的切线方程为
三、填空题
-
15. 对于函数 ,若 ,则a=16. 已知函数 的图象在点 处的切线方程为 ,则 的值为.17. 若抛物线 与直线 相切,则 .18. 与直线 平行且与抛物线 相切的直线方程是 .
四、解答题