广西壮族自治区玉林市玉州区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数： $- 2$ ， $+ 2$ ， $+ 3.5$ ，0， $- \frac{2}{3}$ ， $- 0.7$ ，11， $+ π$ ，其中负数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列计算正确的是（　　）

A、 $3 a + 2 b = 5 a b$ B、 $a + a = a^{2}$ C、 $5 a - 3 a = 2$ D、 $3 a - 2 a = a$

查看试题解析
3. 比1小2的数是（）

A、 $- 3$ B、 $- 2$ C、 $- 1$ D、 $1$

查看试题解析
4. 如果单项式 $- \frac{1}{2} x^{m + 3} y$ 与 $2 x^{4} y^{n + 3}$ 的差是单项式，那么 ${(m + n)}^{2021}$ 的值为（）

A、 $- 1$ B、0 C、1 D、 $2^{2021}$

查看试题解析
5. 若（k﹣5）x^|k|^﹣4﹣6＝0是关于x的一元一次方程，则k的值为（）

A、5 B、﹣5 C、5 或﹣5 D、4 或﹣4

查看试题解析
6. 用四舍五入法得到的近似数1.02×10⁴ ，其精确度为（）

A、精确到十分位 B、精确到十位 C、精确到百位 D、精确到千位

查看试题解析
7. 已知点 $A ， B ， C$ 在数轴上表示的数分别为 $a ， b ， c$ ，点 $C$ 为 $A B$ 的中点， $b < 0 < a$ 且 $a + b > 0$ ，则下列结论中正确的有（）
① $a - b > 0$ ，② $| a | > | b | > | c |$ ，③ $b - c < 0$ ，④ $a + b = 2 c$

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，是一个正方体的表面展开图， $A = x^{3} + x^{2} y + 3 ， B = x^{2} y - 3 ， C = x^{3} - 1 ， D = - (x^{2} y - 6)$ ，且相对两个面所表示的代数式的和都相等，则 $E$ 代表的代数式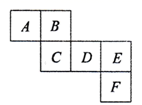是（）

A、 $x^{3} - x^{2} y + 12$ B、10 C、 $x^{3} + 12$ D、 $x^{2} y - 12$

查看试题解析
9. 已知 $x^{2} + 3 x = 2$ ，则多项式 $3 x^{2} + 9 x - 4$ 的值是（）

A、0 B、2 C、4 D、6

查看试题解析
10. 小明骑自行车到学校上学，若每小时骑15千米，可早到10分钟，若每小时骑13千米，则迟到5分钟，设他家到学校的路程为x千米，下列方程正确的是（）

A、 $\frac{x}{15} + \frac{10}{60} = \frac{x}{13} - \frac{5}{60}$ B、 $\frac{x}{15} + 10 = \frac{x}{13} - 5$ C、 $\frac{x}{15} + \frac{10}{60} = \frac{x}{13} + \frac{5}{60}$ D、 $\frac{x}{15} - \frac{10}{60} = \frac{x}{13} - \frac{5}{60}$

查看试题解析
11. 如图，线段 $C D$ 在线段 $A B$ 上，且 $C D = 3$ ，若线段 $A B$ 的长度是一个正整数，则图中以 $A$ ， $B$ ， $C$ ， $D$ 这四点中任意两点为端点的所有线段长度之和可能是（）

A、28 B、29 C、30 D、31

查看试题解析
12. 如图，将两块三角尺 $A O B$ 与 $C O D$ 的直角顶点 $O$ 重合在一起，若 $∠ A O D = 4 ∠ B O C$ ， $O E$ 为 $∠ B O C$ 的平分线，则 $∠ D O E$ 的度数为（）

A、72° B、60° C、45° D、36°

查看试题解析

二、填空题

13. 一个角的度数是 $28 ° 25^{'}$ ，则它的余角等于.

查看试题解析
14. 已知太阳与地球之间的平均距离约为 $\begin{matrix} 150 & 000 & 000 \end{matrix}$ 千米，用科学记数法表示为千米．

查看试题解析
15. 规定“Δ”是一种新的运算法则，满足：a△b=ab-3b，示例：4△（-3）=4×（-3）-3×（-3）=-12+9=-3.若-3△（x+1）=1，则x=.

查看试题解析
16. 如图，将一张长方形纸片 $A B C D$ 分别沿着 $B E$ 、 $B F$ 折叠，使边 $A B$ 、 $C B$ 均落在 $B D$ 上，得到折痕 $B E$ 、 $B F$ ，则 $∠ A B E + ∠ C B F =$ .

查看试题解析
17. 在数轴上点 $A$ 对应的数为 $- 4$ ，点 $B$ 是数轴上的一个动点，当动点 $B$ 到原点的距离与到点 $A$ 的距离之和为10时，则点 $B$ 对应的数为.

查看试题解析
18. 当代数式 ${(x - 3)}^{2} + 8$ 取得最小值时，代数式 $x + 4$ 的值是.

查看试题解析

三、解答题

19. 计算：－1¹⁰⁰ －（1－0.5）× $\frac{1}{3}$ ×[3－（－3）²]

查看试题解析
20. 解方程： $x - \frac{1 - x}{3} = \frac{x + 2}{6} - 1$ .

查看试题解析
21. 先化简，再求值： $4 x^{2} - 2 x y + y^{2} - 2 (x^{2} - x y + 5 y^{2})$ ，其中 $x = 3, y = - 1$ .

查看试题解析
22. 如图，已知 $∠ M O N$ ，按下列要求画图.

(1)、在 $∠ M O N$ 的内部画射线 $O P$ ；

(2)、画 $∠ M O Q$ ，使 $O N$ 在 $∠ M O Q$ 的内部；

(3)、在完成（1）、（2）后，图中共个角，并写角的名称：

查看试题解析
23. 如图， $O$ 是直线 $C E$ 上一点，以 $O$ 为顶点作 $∠ A O B = 90 °$ ，且 $O A$ ， $O B$ 位于直线 $C E$ 两侧， $O B$ 平分 $∠ C O D$ .

(1)、当 $∠ A O C = 50 °$ 时，求 $∠ D O E$ 的度数；

(2)、通过（1）的计算，请你猜想 $∠ A O C$ 和 $∠ D O E$ 的数量关系，并说明理由.

查看试题解析
24. 已知代数式 $M = 3 (a - 2 b) - (b + 2 a)$ .

(1)、化简 $M$ ；

(2)、如果 $(a + 2) x^{2} + 4 x^{b - 2} - 3 = 0$ 是关于 $x$ 的一元一次方程，求 $M$ 的值.

查看试题解析
25. 某商场第一季度销售甲、乙两种冰箱若干台，其中乙种冰箱的数量比甲种冰箱多销售40台，第二季度甲种冰箱的销量比第一季度增加10%，乙种冰箱的销量比第一季度增加20%，且第二季度两种冰箱的总销量达到554台.

(1)、该商场第一季度销售甲种冰箱多少台？

(2)、若每台甲种冰箱的利润为250元，每台乙种冰箱的利润为300元，则该商场第二季度销售冰箱的总利润是多少元？

查看试题解析
26. 已知点 $C$ ，线段 $A B$ .

(1)、如图，若点 $C$ 在线段 $A B$ 上，且 $A C = 12$ ， $B C = 8$ ，点 $M$ 、 $N$ 分别是 $A C$ 、 $B C$ 的中点，则线段 $M N$ 的长度是；

(2)、若把（1）中点 $C$ 在线段 $A B$ 上，且 $A C = 12$ ， $B C = 8$ ，改为点 $C$ 是线段 $A B$ 上任意一点，且 $A C = a$ ， $B C = b$ ，其他条件不变，请求出线段 $M N$ 的长度（用含 $a$ 、 $b$ 的式子表示）；

(3)、若把（2）中点 $C$ 是线段 $A B$ 上任意一点，改为点 $C$ 是直线 $A B$ 上任意一点，其他条件不变，则线段 $M N$ 的长度会变化吗？若有变化，求出结果.

查看试题解析