浙江省台州市仙居县2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 如果把收入300元记作+300元,那么支出200元记作( )A、+100元 B、-200元 C、+200元 D、-100元2. 截至当地时间2021年1月4日,美国累计报告的新冠肺炎确诊病例约21100000人,将数据21100000用科学记数法表示为 ( )A、 B、 C、 D、3. 下列计算结果为负数的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、单项式 的次数是1 B、单项式 的系数是 C、多项式 是三次三项式 D、 与 是同类项5. 下列等式变形正确的是 ( )A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么6. 如图,在正方体的展开图中,与汉字“抗”相对的面上的汉字是( )
 A、共 B、同 C、疫 D、情7. 若 是关于 的方程 的解,则 的值为( )A、-1 B、0 C、1 D、8. 如图,直线 相交于点 , 平分 , ,则 度数为( )
A、共 B、同 C、疫 D、情7. 若 是关于 的方程 的解,则 的值为( )A、-1 B、0 C、1 D、8. 如图,直线 相交于点 , 平分 , ,则 度数为( ) A、125° B、130° C、135° D、145°9. 轮船沿江从甲港逆流行驶到乙港,比从乙港返回甲港多用 ,若船在静水中的速度为 ,水速为为 ,则甲港和乙港相距多少千米?设甲港和乙港相距 ,则下面列出的方程中符合题意的是 ( )A、 B、 C、 D、10. 某水果商店在甲批发市场以每千克 元的价格购进30千克的橘子,又在乙批发市场以每千克 元( )的价格购进同样的50千克橘子.如果以每千克 元的价格全部卖出这种橘子,那么这家商店( )A、盈利了 B、亏损了 C、不盈不亏 D、盈亏不能确定
A、125° B、130° C、135° D、145°9. 轮船沿江从甲港逆流行驶到乙港,比从乙港返回甲港多用 ,若船在静水中的速度为 ,水速为为 ,则甲港和乙港相距多少千米?设甲港和乙港相距 ,则下面列出的方程中符合题意的是 ( )A、 B、 C、 D、10. 某水果商店在甲批发市场以每千克 元的价格购进30千克的橘子,又在乙批发市场以每千克 元( )的价格购进同样的50千克橘子.如果以每千克 元的价格全部卖出这种橘子,那么这家商店( )A、盈利了 B、亏损了 C、不盈不亏 D、盈亏不能确定二、填空题
-
11. 计算: 的结果是.12. 某校组织学生开展献爱心捐款活动,七年级学生捐款 元,八年级学生捐款 元,九年级学生捐款数比七、八年级捐款总数3倍少40元,则九年级学生捐款数为元.13. 如图,已知 , 为线段 的中点,点 在线段 上,且 ,则线段 的长为.
 14. 一个角的补角是它的余角的三倍,则这个角的度数为.15. 已知 ,求 的值是.16. 现有甲、乙、丙三个圆柱形的杯子,杯深均为 ,各装有 高的水,甲、乙、丙三个杯子的底面积如下表.分别从甲、乙两杯中取出相同体积的水倒入丙杯,过程中水没溢出,最后甲、乙两杯水的高度之和等于丙杯水的高度.则从甲杯中倒出的水的体积为 .
14. 一个角的补角是它的余角的三倍,则这个角的度数为.15. 已知 ,求 的值是.16. 现有甲、乙、丙三个圆柱形的杯子,杯深均为 ,各装有 高的水,甲、乙、丙三个杯子的底面积如下表.分别从甲、乙两杯中取出相同体积的水倒入丙杯,过程中水没溢出,最后甲、乙两杯水的高度之和等于丙杯水的高度.则从甲杯中倒出的水的体积为 .底面积( )
甲杯
40
乙杯
60
丙杯
80
三、解答题
-
17. 计算:(1)、 ;(2)、18. 解方程,并在每一步后面写出你的依据.19. 先化简,再求值: ,其中 .20. 如图,在平面内有三个点
 (1)、根据下列语句画图:
(1)、根据下列语句画图:①连接 ;
②作直线 ;
③作射线 ,在 的延长线上取一点 使得 ,连接 ;
(2)、比较 的大小关系.21. 对于有理数 ,定义一种新运算“*”,规定: .(1)、计算 的值;(2)、已知 在数轴上的位置如图所示,若 ,求 的值. 22. 图1是用绳索织成的一片网的一部分,小明为了研究这片网的结点数( ),网眼数( ),边数( )之间的关系,他采用由特殊到一般的方法进行探索,列表如下:
22. 图1是用绳索织成的一片网的一部分,小明为了研究这片网的结点数( ),网眼数( ),边数( )之间的关系,他采用由特殊到一般的方法进行探索,列表如下:特殊网图




结点数( )
4
6
9
12
网眼数( )
1
2
4
6
边数( )
4
7
12
☆
(1)、表中“☆”处应填的数字为;根据上述探索过程,可能猜想 之间满足的数量关系是.(2)、如图2,若网眼形状为六边形,请仿照小明的探索方法,完成下面表格并猜想 之间满足的数量关系.
特殊网图




结点数( )
网眼数( )
边数( )
根据上述探索过程,猜想 之间满足的数量关系.
23. 从一个锐角 顶点出发在角的内部引一条射线,把 分成两个角,若其中一个角与 互余,则这条射线叫做锐角 的余分线,这个角叫做锐角 的余分角.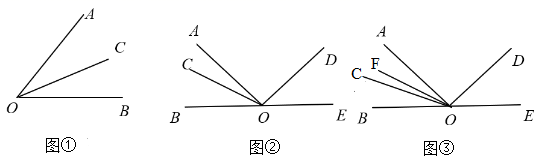 例如:图①中,当 时, 与 互余,那么 是 的余分线, 是 的余分角.(1)、若 , 是它的余分线,则 ;(2)、如图②, 是平角, 是 的余分角, ,试说明 .(3)、如图③,在(2)的条件下,若 是 的平分线, ,求 度数.24. 某市居民生活用电峰谷电价如下表:
例如:图①中,当 时, 与 互余,那么 是 的余分线, 是 的余分角.(1)、若 , 是它的余分线,则 ;(2)、如图②, 是平角, 是 的余分角, ,试说明 .(3)、如图③,在(2)的条件下,若 是 的平分线, ,求 度数.24. 某市居民生活用电峰谷电价如下表:高峰时间段用电价格表
低谷时间段用电价格表
高峰电价(单位:元/千瓦时)
低谷月用电量(单位:千瓦时)
低谷电价(单位:元/千瓦时)
0.56
50及以下部分
0.28
超过50至200的部分
0.32
超过200的部分
0.38
(总用电量=高峰用电量+低谷用电量)
(1)、小明家3月用电量中,高峰用电量为60千瓦时,低谷用电量为40千瓦时,这个月他家需付电费多少元?(2)、如果小明家4月用电总量为 千瓦时( ),高峰用电量为100千瓦时,请分析他家4月份需付的电费(用含字母 的整式表示并化简);(3)、小明家7月用电总量为400千瓦时,需付电费156元,问:这个月小明家高峰用电量和低谷用电量分别用了多少千瓦时?