浙江省绍兴市越城区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 下列四个运算中,结果最小的是( )A、 B、 C、 D、2. 在下列各数0.51515354,0,0. ,3π, ,6.1010010001…, 中,无理数的个数是( )A、1 B、2 C、3 D、43. 十九大报告指出,我国目前经济保持了中高速增长,在世界主要国家中名列前茅,国内生产总值从54万亿元增长80万亿元,稳居世界第二,其中80万亿用科学记数法表示为( )A、8×1012 B、8×1013 C、8×1014 D、0.8×10134. 下列说法中,正确的是( )A、单项式 的系数 B、单项式 的次数为2 C、多项式x2+2xy+18是二次三项式 D、多项式 x3 - x2y2-1次数最高项的系数是5. 下列解方程去分母正确的是( )A、由 ,得2x﹣1=3﹣3x B、由 ,得2x﹣2﹣x=﹣4 C、由 ,得2y-15=3y D、由 ,得3(y+1)=2y+66. 如图,B是线段AD的中点,C是线段BD上一点,则下列结论中错误的是( )
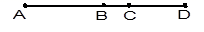 A、BC=AB-CD B、BC= (AD-CD) C、BC= AD-CD D、BC=AC-BD7. 如图,已知∠1=∠2,其中能判定AB∥CD的是( )A、
A、BC=AB-CD B、BC= (AD-CD) C、BC= AD-CD D、BC=AC-BD7. 如图,已知∠1=∠2,其中能判定AB∥CD的是( )A、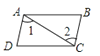 B、
B、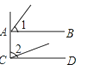 C、
C、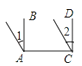 D、
D、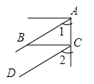 8. 用白铁皮做罐头盒,每张铁皮可制盒身15个或盒底42个,一个盒身与两个盒底配成一套罐头盒. 现有108张白铁皮,用多少张制盒身,多少张制盒底,可以正好制成整套罐头盒?设用 张白铁皮制盒身,可列出方程( )A、 B、 C、 D、9. 下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第几个图形中面积为1的正方形的个数为2019个( )
8. 用白铁皮做罐头盒,每张铁皮可制盒身15个或盒底42个,一个盒身与两个盒底配成一套罐头盒. 现有108张白铁皮,用多少张制盒身,多少张制盒底,可以正好制成整套罐头盒?设用 张白铁皮制盒身,可列出方程( )A、 B、 C、 D、9. 下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第几个图形中面积为1的正方形的个数为2019个( ) A、402 B、403 C、404 D、40510. 将四张边长各不相同的正方形纸片按如图方式放入矩形 内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为 .若知道 的值,则不需测量就能知道周长的正方形的标号为( )
A、402 B、403 C、404 D、40510. 将四张边长各不相同的正方形纸片按如图方式放入矩形 内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为 .若知道 的值,则不需测量就能知道周长的正方形的标号为( )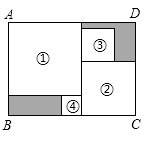 A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
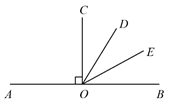
11. 用“>、=、<”符号填空: .12. 的算术平方根是13. 已知2y2+y -2的值为3,则4y2+2y+1的值为14. 已知关于x的一元一次方程0.5x+1=2x+b的解为x=2,那么关于y的一元一次方程0.5(y -1)+1=2(y-1)+b的解为.15. 如图,点O在直线AB上, , , 平分 ,则图中一共有对互补的角.
 16. 如图,点A、点B在数轴上表示的数分别是-4和4.若在数轴上存在一点P到A的距离是点P到B的距离的3倍,则点P所表示的数是 .
16. 如图,点A、点B在数轴上表示的数分别是-4和4.若在数轴上存在一点P到A的距离是点P到B的距离的3倍,则点P所表示的数是 .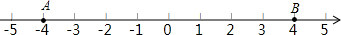 17. 如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
17. 如图,已知CD⊥DA,DA⊥AB,∠1=∠4.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵()
∴∠CDA=90°,∠DAB=90°().
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴(),
∴DF∥AE().
三、解答题
-
18. 计算:(1)、 ;(2)、 .19. 先化简,再求值: ,其中 , .20. 解方程.(1)、 ;(2)、 .21. 如图,点 A在数轴上表示的数是-6,点 B在数轴上表示的数是12
 (1)、线段AB的长为;线段AB的中点表示的数是(2)、点C是数轴上的一个动点,当 AC-3BC=6 时,点 C表示的数是多少?22. 华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
(1)、线段AB的长为;线段AB的中点表示的数是(2)、点C是数轴上的一个动点,当 AC-3BC=6 时,点 C表示的数是多少?22. 华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
20
30
售价(元/件)
25
40
(1)、该超市购进甲、乙两种商品各多少件?(2)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?(3)、该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?23.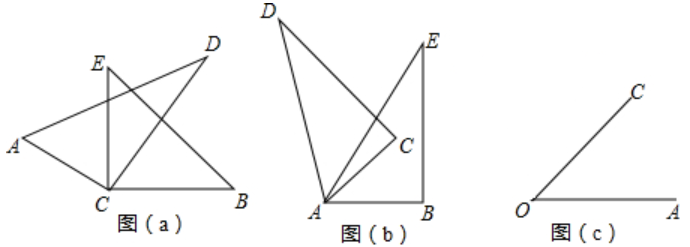 (1)、如图( ),将两块直角三角尺的直角顶点 叠放在一起
(1)、如图( ),将两块直角三角尺的直角顶点 叠放在一起①若 ,求 ;若 ,求 .
②猜想 与 的度数有何特殊关系,并说明理由.
(2)、如图( ),两个同样的三角尺 锐角的顶点 重合在一起,则 与 的度数有何关系?请说明理由.(3)、如图( ),已知 ,作 ( , 都是锐角且 ),若 在 的内部,请直接写出 与 的度数关系.