浙江省宁波市慈溪市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 下列各图中表示线段 ,射线 的是( )A、
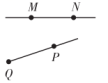
B、
B、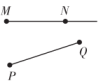
C、
C、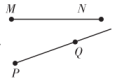
D、
D、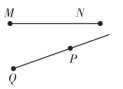
2. 嫦娥五号奔走38万千米外的月球带着“月球标本”飞回地球.数据380000用科学记数法表示为( )A、 B、 C、 D、3. 的倒数与 的相反数的和为( )A、0 B、4 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列判断正确的是( )A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么6. 如图,点 在直线 上, ,那么下列说法错误的是( )
2. 嫦娥五号奔走38万千米外的月球带着“月球标本”飞回地球.数据380000用科学记数法表示为( )A、 B、 C、 D、3. 的倒数与 的相反数的和为( )A、0 B、4 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列判断正确的是( )A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么6. 如图,点 在直线 上, ,那么下列说法错误的是( ) A、 与 相等 B、 与 互余 C、 与 互补 D、 与 互余7. 如图,已知 ,则下列结论中正确的是( )
A、 与 相等 B、 与 互余 C、 与 互补 D、 与 互余7. 如图,已知 ,则下列结论中正确的是( )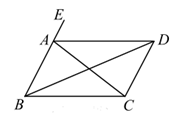 A、 B、 C、 D、8. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:”一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、 =100 B、 =100 C、 D、9. 数轴上有 , , , , 五个点,各点的位置与所表示的数如图所示,且 .若数轴上有一点 , 所表示的数为 ,且 ,则关于点 的位置,下列叙述正确的是( )
A、 B、 C、 D、8. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:”一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、 =100 B、 =100 C、 D、9. 数轴上有 , , , , 五个点,各点的位置与所表示的数如图所示,且 .若数轴上有一点 , 所表示的数为 ,且 ,则关于点 的位置,下列叙述正确的是( )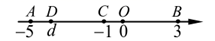 A、 在 , 之间 B、 在 , 之间 C、 在 , 之间 D、 在 , 之间10. 如图,用火柴棍分别搭一排三角形组成的图形和一排正方形组成的图形,三角形、正方形的每一边用一根火柴棒.如果搭这两个图案一共用了2030根火柴棒,且正方形的个数比三角形的个数的少4个,则搭成的三角形的个数是( )
A、 在 , 之间 B、 在 , 之间 C、 在 , 之间 D、 在 , 之间10. 如图,用火柴棍分别搭一排三角形组成的图形和一排正方形组成的图形,三角形、正方形的每一边用一根火柴棒.如果搭这两个图案一共用了2030根火柴棒,且正方形的个数比三角形的个数的少4个,则搭成的三角形的个数是( ) A、429 B、409 C、408 D、404
A、429 B、409 C、408 D、404二、填空题
-
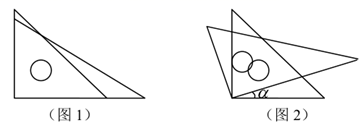
11. 按要求各写出一个数:负整数;无理数.12. 用代数式表示: 与 的平方的和.13. 25的算术平方根为 ,4是 的一个平方根,则 .14. 已知关于 的方程 的解为 ,则 .15. 已知 , ,则 的值为.16. 一副三角板按图1的形式摆放,把含45°角的三角板固定,含30°角的三角板绕直角顶点逆时针旋转,设旋转的角度为 ( ).在旋转过程中,当两块三角板有两边平行时, 的度数为.
三、解答题
-
17. 计算:(1)、 ;(2)、18. 先化简,再求值: ,其中 , .19. 解方程:(1)、 ;(2)、 .20. 如图,已知同一平面内四个点 , , , .
 (1)、同时过 , ,两点能作几条直线?作图并写出理由;(2)、在直线 上画出符合下列条件的点 和 ,并说明理由.
(1)、同时过 , ,两点能作几条直线?作图并写出理由;(2)、在直线 上画出符合下列条件的点 和 ,并说明理由.①使线段 长度最小;
②使 最小.
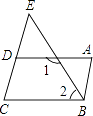
21.如图,已知∠A=∠C,∠1+∠2=180°,试猜想AB与CD之间有怎样的位置关系?并说明理由.
 22. 如图,已知直线 , 相交于点 , 平分 , 平分 .若 ,
22. 如图,已知直线 , 相交于点 , 平分 , 平分 .若 ,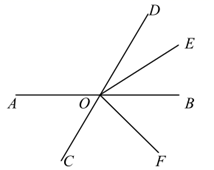 (1)、求 的度数;(2)、求 的度数.23. 小商品批发市场内,某商品的价格按如下优惠:购买不超过300件时,每件3元;超过300件但不超过500件时,每件2.5元;超过500件时,每件2元.某客户欲采购这种小商品700件.(1)、现有两种购买方案:①分两次购买,第一次购买240件,第二次购买460件;②一次性购买700件.问哪种购买方案费用较省?省多少元?说明理由.(2)、若该客户分两次购买该商品共700件(第二次多于第一次),共付费1860元,则第一次、第二次分别购买该商品多少件?24. 给出如下规定:若实数 与 的差等于这两个数的积,则称实数对 为“关联数”.如实数对 ,因为 , ,所以实数对 是关联数;又如实数对 是关联数.(1)、若实数对 为“关联数”,则 , 应满足的条件用含 , 的等式表示为.(2)、判断下列实数对是否是关联数?
(1)、求 的度数;(2)、求 的度数.23. 小商品批发市场内,某商品的价格按如下优惠:购买不超过300件时,每件3元;超过300件但不超过500件时,每件2.5元;超过500件时,每件2元.某客户欲采购这种小商品700件.(1)、现有两种购买方案:①分两次购买,第一次购买240件,第二次购买460件;②一次性购买700件.问哪种购买方案费用较省?省多少元?说明理由.(2)、若该客户分两次购买该商品共700件(第二次多于第一次),共付费1860元,则第一次、第二次分别购买该商品多少件?24. 给出如下规定:若实数 与 的差等于这两个数的积,则称实数对 为“关联数”.如实数对 ,因为 , ,所以实数对 是关联数;又如实数对 是关联数.(1)、若实数对 为“关联数”,则 , 应满足的条件用含 , 的等式表示为.(2)、判断下列实数对是否是关联数?① ;
② .
(3)、若实数对 是关联数,求 的值.(4)、是否存在非零实数 , ,使实数对 与 都是关联数?若存在,求出 , 的值;若不存在,请说明理由.