浙江省嘉兴市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 在 , , , 这四个数中,最小的数是( )A、 B、 C、 D、2. 年 月 日,我国量子计算原型机“九章”问世,它求解数学算法高斯玻色取样只需 秒,而目前世界最快的超级计算机要用 年,数“ ”用科学记数法表示为( )A、 B、 C、 D、3. 下列各组数中,是同类项的是( )A、 与 B、 与 C、 与 D、 与4. 下列关于数的平方根说法正确的是( )A、 的平方根是 B、 的平方根是 C、 的平方根是 D、 没有平方根5. 已知 ,则下列等式不成立的是( )A、 B、 C、 D、6. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
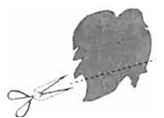 A、垂线段最短 B、经过一点有无数条直线 C、两点之间,线段最短 D、经过两点,有且仅有一条直线7. 某公司 年的销售额为 元,成本为销售额的 ,税额和其它费用合计为销售额的 ,则该公司的年利润可以表示为( )A、 B、 C、 D、8. 将一把直尺和一块三角板如图叠放,直尺的一边刚好经过直角三角板的直角顶点且与斜边相交,则 与 一定满足的数量关系是( )
A、垂线段最短 B、经过一点有无数条直线 C、两点之间,线段最短 D、经过两点,有且仅有一条直线7. 某公司 年的销售额为 元,成本为销售额的 ,税额和其它费用合计为销售额的 ,则该公司的年利润可以表示为( )A、 B、 C、 D、8. 将一把直尺和一块三角板如图叠放,直尺的一边刚好经过直角三角板的直角顶点且与斜边相交,则 与 一定满足的数量关系是( ) A、 B、 C、 D、9. 甲、乙、丙三人进行骑自行车比赛,三人的骑行情况如下表:
A、 B、 C、 D、9. 甲、乙、丙三人进行骑自行车比赛,三人的骑行情况如下表:甲
一半路程速度为 ,一半路程速度为
乙
全程速度均为
丙
一半时间速度为 ,一半时间速度为
设三人到达终点所用时间分别为 、 、 ,则( )
A、 B、 C、 D、10. 小明和小亮在一起探究一个数学活动.首先小亮站立在箱子上,小明站立在地面上(如图1),然后交换位置(如图2),测量的数据如图所示,想要探究的问题有:①小明的身高;②小亮的身高;③箱子的高度;④小明与小亮的身高和.根据图上信息,你认为可以计算出的是( )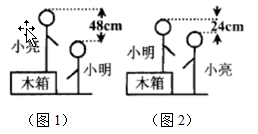 A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
11. 如果涨潮时水位升高 ,水位变化记作 ,那么退潮时水位下降 ,水位变化可记作 .12. 单项式 的系数是.13. 计算: .14. 若 表示 的整数部分,则 .15. 已知关于 的一元一次方程 的解是 ,则 的值为.16. 定义一种新运算: ,则 .17. 小明花费 元购买甲、乙两种水果共 ,已知甲种水果的售价为 元 ,乙种水果的售价为 元 ,设小明购买甲种水果的数量为 ,则根据题意可列方程为.18. 如图, , , 在数轴上对应的点分别为 , , ,其中 ,且 ,则 .
 19. 如图,阶梯图的每个台阶上都标着一个数,从下往上的第 个和第 个台阶上分别标着 和 ,且任意相邻的 个台阶的数的和都等于 ,则从下往上的第 个台阶上的数字是.
19. 如图,阶梯图的每个台阶上都标着一个数,从下往上的第 个和第 个台阶上分别标着 和 ,且任意相邻的 个台阶的数的和都等于 ,则从下往上的第 个台阶上的数字是.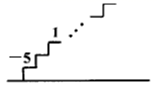 20. 小方同学设计了一个“魔法棒转不停”程序,如图所示,点 , 在直线 上,第一步, 绕点 顺时针旋转 度 至 ;第二步, 绕点 顺时针旋转 度至 ;第三步, 绕点 顺时针旋转 度至 , 以此类推,在旋转过程中若碰到直线 则立即绕点 反方向旋转.当 时,则 等于度.
20. 小方同学设计了一个“魔法棒转不停”程序,如图所示,点 , 在直线 上,第一步, 绕点 顺时针旋转 度 至 ;第二步, 绕点 顺时针旋转 度至 ;第三步, 绕点 顺时针旋转 度至 , 以此类推,在旋转过程中若碰到直线 则立即绕点 反方向旋转.当 时,则 等于度.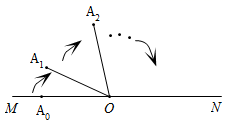
三、解答题
-
21. 计算:(1)、(2)、22. 如图,已知 , , 是平面上不共线的三点.用直尺和圆规作图:

①画射线 ,线段 ;
②在射线 上作出一点 ,使得 .
(不写作法,保留作图痕迹)
23. 先化简,再求值: ,其中 .24. 解方程:(1)、(2)、25. 将一副三角板如图1摆放, , , 平分 , 平分 . (1)、 ;(2)、将图1的三角板 绕点 逆时针旋转 度至图2位置.
(1)、 ;(2)、将图1的三角板 绕点 逆时针旋转 度至图2位置.①当 时,求 的度数.
②当 时,请直接写出 , , 之间的数量关系.
26. 小嘉和小海相约去某景区游玩,其地理位置及部分路线如图1. , , 为三个高速路口,已知高速路段 的路程为 ,在高速上小海每小时可比小嘉多行驶 ,在其余道路上两人的开车速度均为 .他俩的微信对话部分信息如图2.(注:在高速上匀速行驶) (1)、小海从小嘉家开车到高速路口 需要多少时间?(2)、求小海在高速上的行驶速度.(3)、在返回过程中为节省高速路费,小海从 下高速,先送小嘉回家后再返回自己家,发现整个返回过程与整个前往景区过程的时间相同,求小嘉家与小海家之间的距离.
(1)、小海从小嘉家开车到高速路口 需要多少时间?(2)、求小海在高速上的行驶速度.(3)、在返回过程中为节省高速路费,小海从 下高速,先送小嘉回家后再返回自己家,发现整个返回过程与整个前往景区过程的时间相同,求小嘉家与小海家之间的距离.