浙江省湖州市长兴县2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-09 类型：期末考试

进入出卷网下载

一、单选题

1. 2021的倒数是（）

A、 $- 2021$ B、 $- \frac{1}{2021}$ C、2021 D、 $\frac{1}{2021}$

查看试题解析
2. 下列选项是无理数的为（）

A、 $- \frac{1}{3}$ B、 $\sqrt{4}$ C、3.1415926 D、 $- π$

查看试题解析
3. 世界实时统计数据显示，截至北京时间2020年12月7日，全球新冠肺炎累计确诊病例超过67300000例，数67300000用科学记数法表示是（）

A、 $673 \times 10^{5}$ B、 $67.3 \times 10^{6}$ C、 $6.73 \times 10^{7}$ D、 $6.73 \times 10^{8}$

查看试题解析
4. 下列算式中，积为负数的是（）

A、 $0 \times (- 5)$ B、 $4 \times (- 0.5) \times (- 10)$ C、 $(- 1.5) \times (- 2)$ D、 $(- 2) \times (- \frac{1}{5}) \times (- \frac{2}{3})$

查看试题解析
5. 把一根木条固定在墙面上，至少需要两枚钉子，这样做的数学依据是（）

A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、两点之间直线最短

查看试题解析
6. 下列各式的计算，正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $2 y^{2} - y^{2} = 2$ C、 $- 10 t + 5 t = - 5 t$ D、 $3 m^{2} n - 2 m n^{2} = m n$

查看试题解析
7. 如图，若数轴上的点A，B，C，D分别表示数 $- 1$ ，1，2，3，则表示数 $4 - \sqrt{13}$ 的点应在（）

A、点A与点O之间 B、点O与点B之间 C、点B与点C之间 D、点C与点D之间

查看试题解析
8. 一艘轮船在静水中的速度为20km/h，水流速度为4km/h，从甲码头顺流航行到乙码头，再返回甲码头，共用5小时，求甲、乙两码头间的距离.设两码头间的距离为 $x$ km，则下列方程正确的是（）

A、 $(20 + 4) x + (20 - 4) x = 5$ B、 $20 x + 4 x = 5$ C、 $\frac{x}{20} + \frac{x}{4} = 5$ D、 $\frac{x}{24} + \frac{x}{16} = 5$

查看试题解析
9. 如图，一个大正方形的四个角落分别放置了四张大小不同的正方形纸片，其中①，②两张正方形纸片既不重叠也无空隙.已知①号正方形边长为a，②号正方形边长为b，则阴影部分的周长是（）

A、 $2 a + 2 b$ B、 $4 a + 2 b$ C、 $2 a + 4 b$ D、 $3 a + 3 b$

查看试题解析
10. 将连续正整数按如图所示的位置顺序排列：根据排列规律，则2021应在（）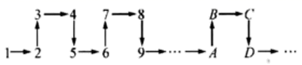

A、A处 B、B处 C、C处 D、D处

查看试题解析

二、填空题

11. 计算： $(- 7) - | - 4 | =$ .

查看试题解析
12. 单项式- $\frac{x^{2} y}{4}$ 的系数是.

查看试题解析
13. 若 $x = - 2$ 是方程 $2 x + m - 4 = 0$ 的解，则m的值是.

查看试题解析
14. 如图，点O在直线 $D B$ 上.已知 $∠ 1 = 25 °$ ， $∠ A O C = 90 °$ ，则 $∠ 2$ 的度数是.

查看试题解析
15. 如果代数式x²+2x的值为5，那么代数式2x²+4x﹣3的值等于

查看试题解析
16. 已知甲沿周长为250米的环形跑道按逆时针方向跑步，与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步，速度为5米秒.当运动时间是50秒时，甲，乙两人第1次相遇，则甲的速度是米/秒.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{16} + (- 8) \div 2$ ；

(2)、 $- 2^{2} \div (- 4) - 12 \times (\frac{1}{2} - \frac{1}{3})$ .

查看试题解析
18. 解方程：

(1)、 $2 x + 1 = 3$ ；

(2)、 $\frac{3 x + 1}{3} - \frac{x - 3}{6} = 5$ .

查看试题解析
19. 先化简，再求值： $2 (a^{2} - a b) - 3 (\frac{2}{3} a^{2} - a b - 1)$ ，其中 $a = - 2, b = 3$

查看试题解析
20. 已知线段 $C D$ ，延长线段 $C D$ 到B，使 $D B = \frac{1}{2} C B$ ，延长 $D C$ 到A，使 $A C = 2 D B$ ，若 $A B = 8 cm$ ，求 $C D$ 与 $A D$ 的长.

查看试题解析
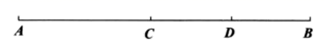21. 一只蚂蚁从点P出发，在一条水平直线上来回匀速爬行.记向右爬行的路程为正，向左爬行的路程为负，爬行的路程依次为（单位：厘米）： $+ 7 ， - 6 ， - 5 ， - 6 ， + 13 ， - 3$ .

(1)、请通过计算说明蚂蚁最后是否回到了起点P.

(2)、若蚂蚁爬行的速度是0.5厘米/秒，问蚂蚁共爬行了多少时间？

查看试题解析
22. 已知，如图直线 $A B$ 与 $C D$ 相交于点O， $O E ⊥ A B$ ，过点O作射线 $O F$ ， $∠ A O D = 30 °$ ， $∠ F O B = ∠ E O C$ .

(1)、求 $∠ E O C$ 度数；

(2)、求 $∠ D O F$ 的度数；

(3)、直接写出图中所有与 $∠ A O D$ 互补的角.

查看试题解析
23. 某城市平均每天产生垃圾700吨，由甲，乙两个垃圾处理厂处理.已知甲厂每小时可以处理垃圾55吨，每吨需费用10元；乙厂每小时可以处理垃圾45吨，每吨费用9元.

(1)、甲，乙两厂同时处理该城市的垃圾，每天需要多少时间完成？

(2)、如果该城市每天用于处理垃圾的费用为6700元，那么甲厂每天处理垃圾多少吨？

查看试题解析
24. 如图，已知在数轴上A点表示数 $- 3$ ，B点表示数1，C点表示数9.

(1)、若将数轴折叠，使得A点与C点重合，则点B与表示数表示的点重合；

(2)、若点A，点B和点C分别以每秒2个单位长度，1个单位长度和4个单位长度的速度在数轴上同时向左运动，点A，点B和点C运动后的对应点分别是点 $A_{1}$ ，点 $B_{1}$ 和点 $C_{1}$ .
①假设t秒钟过后， $A_{1} ， B_{1} ， C_{1}$ 三点中恰有一点为另外两点的中点，求t的值；

②当点 $C_{1}$ 在 $B_{1}$ 点右侧时， $m \cdot B_{1} C_{1} + 3 A_{1} B_{1}$ 的值是个定值，求此时m的值.

查看试题解析