浙江省湖州市南浔区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-09 类型：期末考试

进入出卷网下载

一、单选题

1. -2021的倒数是（）

A、 $- \frac{1}{2021}$ B、 $\frac{1}{2021}$ C、2021 D、-2021

查看试题解析
2. 2020年，南浔开发区抓紧长三角一体化机遇，实施招商引资“一号工程”.1月至11月，签约亿元以上工业项目51个，总投资534.9亿元，534.9亿用科学记数法表示为（）

A、 $534.9 \times 10^{8}$ B、 $5.349 \times 10^{9}$ C、 $0.5349 \times 10^{11}$ D、 $5.349 \times 10^{10}$

查看试题解析
3. 下列各数： $3.1415926 ， \sqrt{8}, \frac{2}{7}, 2.121221 \dots$ （两个1之间依次多一个2）， $- 2 π ， \sqrt[3]{8}, 2021$ 中，有理数的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 下列各式中，不相等的是（）

A、 ${(- 2021)}^{2}$ 和 $- 2021^{2}$ B、 ${(- 2021)}^{2}$ 和 $2021^{2}$ C、 ${(- 2021)}^{3}$ 和 $- 2021^{3}$ D、 $| - 2021 |^{3}$ 和 $| - 2021^{3} |$

查看试题解析
5. 如果 $3 a^{2} b^{2 m - 1}$ 与 $- 2 a^{2} b^{m + 2}$ 是同类项，则m的值为（）

A、1 B、3 C、 $- 1$ D、 $- 3$

查看试题解析
6. 一元一次方程 $\frac{2 x - 1}{3} - \frac{5 x + 2}{6} = 2$ ，去分母后变形正确的是（）

A、 $4 x - 2 - 5 x + 2 = 2$ B、 $4 x - 2 - 5 x - 2 = 2$ C、 $4 x - 2 - 5 x + 2 = 12$ D、 $4 x - 2 - 5 x - 2 = 12$

查看试题解析
7. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”.如图，浔浔在从右到左依次排列的绳子上打结，满七进一，用来记录立志为中考奋斗后努力的天数，由图可知，浔浔努力的天数是（）

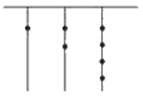A、124 B、469 C、67 D、210

查看试题解析
8. 已知关于x的方程 $2 x + a - 7 = 0$ 的解是 $x = 2$ ，则a的值为（）

A、2 B、3 C、4 D、5

查看试题解析
9. 把9个数填入 $3 \times 3$ 方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”.它源于我国古代的“洛書”（图①），是世界上最早的“幻方”.图②是仅可以看到部分数值的“九宫格”，则其x的值为（）

图②

x

$- 5$

$- 2$

0

1

A、2 B、 $- 1$ C、 $- 3$ D、 $- 4$

查看试题解析
10. 水池 $A, B, C$ 都是长方体，深为 $1.6 m$ ，底部尺寸为 $3 m \times 4 m$ .1号阀门 $24 min$ 可将无水A池注满；2号阀门用来从A池向B池放水， $30 min$ 可将A池中满池水放入B池；3号阀门用来从B池向C池放水， $48 \min$ 可将B池中满池水放入C池.若开始 $A 、 B 、 C$ 三池无水，同时打开1号、2号和3号阀门，那么当B池水深 $0.4 m$ 时，A池有（） $m^{3}$ 的水.

A、1.2 B、3.2 C、6 D、16

查看试题解析

二、填空题

11. $- 3 + 2 =$ .

查看试题解析
12. 9的算术平方根是．

查看试题解析
13. 已知 $∠ α = 50^{°} 30^{'}$ ，则 $∠ α$ 的余角的度数是.

查看试题解析
14. 如图，把一张长方形纸条 $A B C D$ 沿 $E F$ 折叠，若 $∠ A E D^{'} = 68 °$ ，则 $∠ A E F =$ .

查看试题解析
15. 由一些正整数组成的数表如下（表中下一行中数的个数是上一行中数的个数的2倍）：

第1行

2

第2行

4 6

第3行

8 10 12 14

若规定坐标号 $(m ， n)$ 表示第m行从左向右第n个数，则 $(5 ， 6)$ 所表示的数是；数2022对应的坐标号是.

查看试题解析
16. 将长为4宽为a（a大于1且小于4）的长方形纸片按如图所示的方式折叠并压平，剪下一个边长等于长方形宽的正方形，称为第一次操作；再把剩下的长方形按同样的方式操作，称为第二次操作；如此反复操作下去，若在第n次操作后，剩下的长方形恰为正方形，则操作终止.当 $n = 3$ 时，a的值为.

查看试题解析
17. 下列图形是由同样大小的灰、白两种不同颜色的小正方形地砖铺设而成，每一个小正方形表示一块地砖，如果按图1、2、3 的次序铺设地砖，把第n个图形用图n表示，那么图100中的白色小正方形地砖的块数是.

查看试题解析

三、解答题

18. 计算： ${(- 3)}^{2} - 2 \times \sqrt{16}$ .

查看试题解析
19. 解方程： $2 x - 3 (4 - x) = 8$ .

查看试题解析
20. 先化简，再求值： $- 2 (2 x^{2} - x y + \frac{1}{2}) - 3 (x^{2} - x y)$ ，其中 $x = - 1 ， y = 1$ .

查看试题解析
21. 如图，汽车站、码头分别位于 $A ， B$ 两点，直线b和波浪线分别表示公路与河流.

(1)、从汽车站A到码头B怎样走最近？画出最近路线，并说明理由；

(2)、从码头B到公路b怎样走最近？画出最近路线 $B C$ ，并说明理由.（温馨提示：请画在答题卷相对应的图上）

查看试题解析
22. 如图，已知直线 $A B$ 与 $C D$ 相交于点 $O ， O E ⊥ C D ， ∠ A O C = 40^{°} ， O F$ 为 $∠ A O D$ 的角平分线.

(1)、求 $∠ E O B$ 的度数；

(2)、求 $∠ E O F$ 的度数.

查看试题解析
23. 定义一种新运算，规定 $a ⊙ b = | a + b | + | a - b |$ .

(1)、计算 $1 ⊙ (- 3)$ 的值；

(2)、表示数m的点M在数轴上的位置如图所示，且 $2 ⊙ m = 6$ ，求m的值.

查看试题解析
24. 为打造“水晶晶南浔”，实现河流“清如许”，南浔区设立若干河流排污治理点（每处需安装相同长度的排污治理管道）.由甲、乙两工程队同时开工，一天甲队3名工人去完成7个治理点管道铺设，但还有90米管道未来得及完成，同时，乙队4名工人完成7个治理点后，仍多铺设了70米管道，每名甲工人比乙工人一天多铺设40米管道.

(1)、求每个排污治理点需铺设的管道长度；

(2)、已知每位甲工人每天需支付费用500元，每名乙工人每天需支付400元，我区共设立50个排污治理点，另有5940米的同样的污水排放管道也需要安装，现有甲队3名工人，乙队4名工人来安装管道，现有三种方案，方案一：全部由甲队安装；方案二：全部由乙队安装；方案三：甲乙两队一起完成（不到一天按一天算），若要使总费用最少，应选择哪种方案？请通过计算说明.

查看试题解析
25. 操作探究：将两块相同的直角三角板（含有 $30^{°} ， 60^{°}$ 角）如图1摆放在直线 $A D$ 上，三角板 $O M N$ 绕点O以每秒 $10^{°}$ 的速度顺时针旋转，当 $O N$ 旋转至与射线 $O A$ 重合时停止.设旋转时间为t秒.

(1)、若三角板 $O B C$ 保持不动，如图2，当 $t = 3$ 时，试判断 $∠ A O M$ 和 $∠ B O M$ 是否相等，并说明理由；

(2)、若两块三角板同时旋转，三角板 $O B C$ 以每秒 $5^{°}$ 的速度绕点O顺时针旋转，当 $O B$ 旋转至与射线 $O D$ 重合时停止.
①在三角板 $O B C$ 停止运动之前，求 $∠ A O M$ 和 $∠ A O B$ 的度数（用含t的代数式表示）；

②定义：能把一个角分成 $1 ： 2$ 的两部分的直线叫做该角的三分线，当直线 $O M$ 为 $∠ A O B$ 的三分线时，求t的值.

查看试题解析
26. 已知 $p 、 q 、 r$ 为质数， $p < q ， p + q = r$ ，若下图中 $A C$ 线段的长为 $p ， D$ 是线段 $A B$ 的中点，且图中所有线段长度之和为33，求线段 $A B$ 的长.

查看试题解析

第1行	2
第2行	4 6
第3行	8 10 12 14