广西壮族自治区来宾市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 甲、乙、丙三地的海拔高度分别为 , 和 ,那么最高的地方比最低的地方高( )A、 B、 C、 D、2. 为了解甲、乙、丙、丁四所学校学生对“122交通安全专题”相关知识的掌握情况,小明计划进行抽样调查,你认为以下方案中最合理的是( )A、抽取甲校七年级学生进行调查 B、在四个学校随机抽取200名老师进行调查 C、在乙校中随机抽取200名学生进行调查 D、在四个学校各随机抽取200名学生进行调查3. 运用等式的性质变形正确的是( )A、如果a=b,那么a+c=b﹣c B、如果a=3,那么a2=3a2 C、如果a=b,那么 = D、如果 = ,那么a=b4. 今年6月13日是我国第四个文化和自然遗产日.目前我国世界遗产总数居世界首位,其中自然遗产总面积约68000km2.将68000用科学记数法表示为( )A、6.8×104 B、6.8×105 C、0.68×105 D、0.68×1065. 下列计算正确的是( )A、 B、 C、 D、6. 已知点A在数轴上表示的数是 ,则距离A点3个单位的点所表示的数是( )A、0 B、1或0 C、0或 D、0或7. 已知-25a2mb和7b3-na4是同类项,则m+n的值是( )
A、2 B、3 C、4 D、68. 如果一个角的补角是 ,那么这个角的余角是( )A、 B、 C、 D、9. 若x=2是关于x的一元一次方程ax-2=b的解,则3b-6a+2的值是( ).A、-8 B、-4 C、8 D、410. 如图,C是线段AB上的点,D是线段AC的中点,E是线段BC的中点,若DE=10,则AB的长为( ) A、10 B、20 C、30 D、4011. 小文在做多项式减法运算时,将减去 误认为是加上 ,求得的答案是 (其他运算无误),那么正确的结果是( )A、 B、 C、 D、12. 小张在做数学题时,发现了下面有趣的结果
A、10 B、20 C、30 D、4011. 小文在做多项式减法运算时,将减去 误认为是加上 ,求得的答案是 (其他运算无误),那么正确的结果是( )A、 B、 C、 D、12. 小张在做数学题时,发现了下面有趣的结果……
根据以上规律可知,第20行左起第一个数是( )
A、360 B、339 C、440 D、483二、填空题
-
13. 的倒数是.14. 的最高次项为.15. 如图,已知长方形的长为 ,宽为 ,用代数式表示图中阴影部分的面积为.
 16. 如图是一个正方体的表面展开图,已知正方体的每一个面都有一个有理数,且相对面上的两个数互为相反数,那么代数式 的值等于.
16. 如图是一个正方体的表面展开图,已知正方体的每一个面都有一个有理数,且相对面上的两个数互为相反数,那么代数式 的值等于. 17. 某工艺品车间有20名工人,平均每人每天可制作12个大花瓶或10个小饰品,已知2个大花瓶与5个小饰品配成一套,则要安排名工人制作大花瓶,才能使每天制作的大花瓶和小饰品刚好配套.18. 如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第n个图中正方形和等边三角形的个数之和为个.
17. 某工艺品车间有20名工人,平均每人每天可制作12个大花瓶或10个小饰品,已知2个大花瓶与5个小饰品配成一套,则要安排名工人制作大花瓶,才能使每天制作的大花瓶和小饰品刚好配套.18. 如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第n个图中正方形和等边三角形的个数之和为个.
三、解答题
-
19. 计算与解方程(1)、计算: ;(2)、解方程: .20. 如图,已知 , , , 四个点,按要求画出图形.
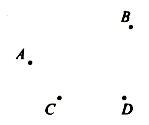 (1)、①画直线 , 相交于点 ;
(1)、①画直线 , 相交于点 ;②画射线 :
③连接 ;
(2)、图中共有条线段.21. 某地教研部门为了解本地区学生在“停课不停学”在线学习期间的学习情况,进行了如下调查:要求每名学生在“优秀”,“良好”,“一般”和“较差”这四个选项中选择一项进行自我评价.调查组随机抽取了若干名学生的问卷进行统计并绘制如图所示的两幅不完整统计图.

请根据图中所给信息,解答下列问题:
(1)、在这次调查中,一共抽查了名学生;(2)、在扇形统计图中,求“良好”所对应的圆心角的度数;(3)、请将条形统计图补充完整.22. 如图,已知点O是直线AB上的一点, ,OD、OE分别是 、 的角平分线. (1)、求 的度数;(2)、写出图中与 互余的角;(3)、图中有 的补角吗?若有,请把它找出来,并说明理由.23. 已知: , , , ,求 的值.24. 数轴上点 分别对应数 ,其中 , .
(1)、求 的度数;(2)、写出图中与 互余的角;(3)、图中有 的补角吗?若有,请把它找出来,并说明理由.23. 已知: , , , ,求 的值.24. 数轴上点 分别对应数 ,其中 , . (1)、若 , ,则线段 的中点对应的数是;(直接填结果)(2)、若 , ,且 ,请在数轴上画出点 ,并求 的值.25. 已知将一副三角尺(直角三角尺 和 )的两个顶点重合于点 , ,
(1)、若 , ,则线段 的中点对应的数是;(直接填结果)(2)、若 , ,且 ,请在数轴上画出点 ,并求 的值.25. 已知将一副三角尺(直角三角尺 和 )的两个顶点重合于点 , , (1)、如图1,将三角尺 绕点 逆时针方向转动,当 恰好平分 时,求 的度数;(2)、如图2,当三角尺 摆放在 内部时,作射线 平分 ,射线 平分 ,如果三角尺 在 内绕点 任意转动, 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.26. 某市 , 两仓库分别有水泥15吨和35吨, , 两工地分别需要水泥20吨和30吨.已知从 , 仓库到 , 工地的运价如下表:
(1)、如图1,将三角尺 绕点 逆时针方向转动,当 恰好平分 时,求 的度数;(2)、如图2,当三角尺 摆放在 内部时,作射线 平分 ,射线 平分 ,如果三角尺 在 内绕点 任意转动, 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.26. 某市 , 两仓库分别有水泥15吨和35吨, , 两工地分别需要水泥20吨和30吨.已知从 , 仓库到 , 工地的运价如下表:工地
仓库
工地
工地
仓库
每吨15元
每吨12元
仓库
每吨10元
每吨9元
若从 仓库运到 工地的水泥为 吨.
(1)、用含 的式子表示从 仓库运到 工地的水泥的数量,从 仓库运到 工地的运输费用;(2)、求把全部水泥从 , 两仓库运到 , 两工地的总运输费(用含 的式子表示):(3)、当总运输费为535元时,水泥该如何运输调配?