浙江省台州市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-09 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $△ A B C$ 中， $∠ C = 90^{\circ}$ ， $cos A = \frac{3}{5}$ ，那么 $sin A$ 的值等于（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
2. 抛掷一枚质地均匀的硬币，若抛掷95次都是正面朝上，则抛掷第100次正面朝上的概率是（）

A、小于 $\frac{1}{2}$ B、等于 $\frac{1}{2}$ C、大于 $\frac{1}{2}$ D、无法确定

查看试题解析
3. 函数y=﹣2x²先向右平移1个单位，再向下平移2个单位，所得函数解析式是（）

A、y=﹣2（x﹣1）²+2 B、y=﹣2（x﹣1）²﹣2 C、y=﹣2（x+1）²+2 D、y=﹣2（x+1）²﹣2

查看试题解析
4. 若反比例函数 $y = \frac{k}{x}$ 的图象经过 $(- 1, 3)$ ，则这个函数的图象一定过（）

A、 $(- 3, 1)$ B、 $(- \frac{1}{3}, 3)$ C、 $(- 3, - 1)$ D、 $(\frac{1}{3}, 3)$

查看试题解析
5. 如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC＝25°，则∠CAD的度数为（）

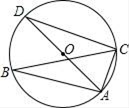A、25° B、50° C、65° D、75°

查看试题解析
6.
如图，在△ABC与△ADE中，∠BAC=∠D，要使△ABC与△ADE相似，还需满足下列条件中的（　　）

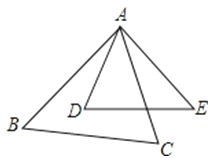A、 $\frac{A C}{A D}$ = $\frac{A B}{A E}$ B、 $\frac{A C}{A D}$ = $\frac{B C}{D E}$ C、 $\frac{A C}{A D}$ = $\frac{A B}{D E}$ D、 $\frac{A C}{A D}$ = $\frac{B C}{A E}$

查看试题解析
7. 如图1，在Rt△ABC中，∠B＝90°，∠ACB＝45°，延长BC到D，使CD＝AC，则tan22.5°＝（）

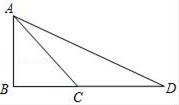A、 $\sqrt{2} + 1$ B、 $\sqrt{2} - 1$ C、 $\frac{\sqrt{2} + 1}{2}$ D、 $\frac{\sqrt{2} - 1}{2}$

查看试题解析
8. 如图，圆内接四边形ABCD的边AB过圆心O，过点C的切线AD的延长线交于点E，若点D是弧AC的中点，且∠ABC=70°，则∠AEC等于（）

A、80° B、75° C、70° D、65°

查看试题解析
9. 如图，在平面直角坐标系中，Rt△ABC的顶点，B分别在y轴、x轴上，OA＝2，OB＝1，斜边AC∥x轴.若反比例函数（k＞0，x＞0）的图象经过AC的中点D，则k的值为（）

A、8 B、5 C、6 D、4

查看试题解析
10. 对于实数a、b，定义运算“★”：a★b= ${\begin{array}{l} a^{2} - b (a \leq b) \\ b^{2} - a (a > b) \end{array}$ ，关于x的方程（2x+1）★（2x-3）=t恰好有两个不相等的实数根，则t的取值范围是（）

A、t＜ $\frac{15}{4}$ B、t＞ $\frac{15}{4}$ C、t＜ $- \frac{17}{4}$ D、t＞ $- \frac{17}{4}$

查看试题解析

二、填空题

11. 二次函数y=x²﹣2x+3图象的顶点坐标为．

查看试题解析
12. 一个盒中装着大小、外形一模一样的x颗白色弹珠和y颗黑色弹珠，从盒中随机取出一颗弹珠，取得白色弹珠的概率是 $\frac{1}{3}$ .如果再往盒中放进12颗同样的白色弹珠，取得白色弹珠的概率是 $\frac{2}{3}$ ，则原来盒中有白色弹珠颗.

查看试题解析
13. 用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

查看试题解析
14. 如图，l₁∥l₂∥l₃ ，且l₁ ， l₂之间的距离为2，l₂ ， l₃之间的距离为3.若点A，B，C分别在直线l₁ ， l₂ ， l₃上，且AC⊥BC，AC＝BC，则AB的长是.

查看试题解析
15. 如图，一次函数 $y = a x + b$ 的图象交x轴于点B，交y轴于点A，交反比例函数 $y = \frac{k}{x}$ 的图象于点 $C$ ，若 $A B = B C$ ，且 $△ OAC$ 的面积为2，则k的值为

查看试题解析
16. 如图，AB为半圆O的直径，M，C是半圆上的三等分点，AB＝8，BD与半圆O相切于点B.点P为 $\hat{AM}$ 上一动点（不与点A，M重合），直线PC交BD于点D，BE⊥OC于点E，延长BE交PC于点F，则下列结论正确的是.（写出所有正确结论的序号）
①PB＝PD；② $\hat{BC}$ 的长为 $\frac{4}{3}$ π；③∠DBE＝45°；④△BCF∽△PFB；⑤CF•CP为定值.

查看试题解析

三、解答题

17. 计算： $2 \cos 45^{\circ} - 6 \tan^{2} 30^{\circ} - \sqrt{3} \sin 60^{\circ}$ .

查看试题解析
18. 太阳能光伏发电因其清洁、安全、便利、高效等特点，已成为世界各国普遍关注和重点发展的新兴产业，如图是太阳能电池板支撑架的截面图，其中的粗线表示支撑角钢，太阳能电池板与支撑角钢AB的长度相同，均为300cm，AB的倾斜角为 $30 °$ ，BE=CA=50cm，支撑角钢CD，EF与底座地基台面接触点分别为D，F，CD垂直于地面， $F E ⊥ A B$ 于点E.两个底座地基高度相同（即点D，F到地面的垂直距离相同），均为30cm，点A到地面的垂直距离为50cm，求支撑角钢CD和EF的长度各是多少cm（结果保留根号）

查看试题解析
19. 如图，△ABC内接于⊙O，AB为直径，∠BAC=60°，延长BA至点P使AP=AC，作CD平分∠ACB交AB于点E，交⊙O于点D. 连结PC，BD.

(1)、求证：PC为⊙O的切线；

(2)、求证：BD= $\sqrt{2}$ PA；

(3)、若PC= $6 \sqrt{3}$ ，求AE的长.

查看试题解析
20. 如图，已知反比例函数y＝ $\frac{k}{x}$ 的图象与一次函数y＝x+b的图象交于点A(1，4)，点B(﹣4，n).

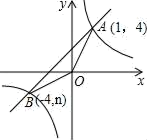(1)、求n和b的值；

(2)、求△OAB的面积；

(3)、直接写出一次函数值大于反比例函数值的自变量x的取值范围.

查看试题解析
21. 某中学开展了四项体育锻炼活动：A：篮球；B：足球；C：跳绳；D：跑步．陈老师对学生最喜欢的一项体育锻炼活动进行了抽样调查（每人只限一项），并将调查结果绘制成图 1，图2两幅不完整的统计图．

请根据图中信息解答下列问题：

(1)、参加此次调查的学生总数是人；将图1、图2的统计图补充完整；

(2)、已知在被调查的最喜欢篮球的3名学生中只有1名男生，现从这3名学生中任意抽
取2名学生参加校篮球队，请用列表法或画树状图的方法，求出恰好抽到两名女生的概率．

查看试题解析
22. 定义：连结菱形的一边中点与对边的两端点的线段把它分成三个三角形，如果其中有两个三角形相似，那么称这样的菱形为自相似菱形.

(1)、判断下列命题是真命题，还是假命题？
①正方形是自相似菱形；

②有一个内角为60°的菱形是自相似菱形.

③如图1，若菱形ABCD是自相似菱形，∠ABC=α(0°＜α＜90°)，E为BC中点，则在△ABE，△AED，△EDC中，相似的三角形只有△ABE与△AED.

(2)、如图2，菱形ABCD是自相似菱形，∠ABC是锐角，边长为4，E为BC中点.
①求AE，DE的长；

②AC，BD交于点O，求tan∠DBC的值.

查看试题解析
23. 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．

(1)、当销售单价为70元时，每天的销售利润是多少？

(2)、求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式，并求出自变量x的取值范围；

(3)、如果该企业每天的总成本不超过7000元，那么销售单价为多少元时，每天的销售利润最大？最大利润是多少？（每天的总成本=每件的成本×每天的销售量）

查看试题解析
24. 如图，A，B，C，D四点都在OO上，弧AC＝弧BC，连接AB，CD、AD，∠ADC＝45°.

(1)、如图1，AB是⊙O的直径；

(2)、如图2，过点B作BE⊥CD于点E，点F在弧AC上，连接BF交CD于点G，∠FGC＝2∠BAD，求证：BA平分∠FBE；

(3)、如图3，在（2）的条件下，MN与⊙O相切于点M，交EB的延长线于点N，连接AM，若2∠MAD+∠FBA＝135°，MN＝ $\frac{10}{13}$ AB，EN＝26，求线段CD的长.

查看试题解析