浙江省绍兴市上虞区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-09 类型:期末考试
一、单选题
-
1. 已知二次函数 ,当 时,函数值是-5,则下列关于 , 的关系式中,正确的是( )A、 B、 C、 D、2. 如图,在 中, ,则下列比例式一定正确的是( )
 A、 B、 C、 D、3. 下列各事件中,是随机事件的是( )A、 是实数,则 . B、某运动员跳高的最好成绩是10.1m. C、从装有多个白球的箱子里取出2个红球. D、从车间刚生产的产品中任意抽一个,是次品.4. 如图,已知 ,则图中角度 和边长 分别为( )
A、 B、 C、 D、3. 下列各事件中,是随机事件的是( )A、 是实数,则 . B、某运动员跳高的最好成绩是10.1m. C、从装有多个白球的箱子里取出2个红球. D、从车间刚生产的产品中任意抽一个,是次品.4. 如图,已知 ,则图中角度 和边长 分别为( )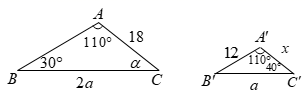 A、40°,9 B、40°,6 C、30°9 D、30°,65. 使用家用燃气灶烧开同一壶水所需的燃气量 (单位: )与旋钮的旋转角度 (单位:度)( )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度 与燃气量 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A、40°,9 B、40°,6 C、30°9 D、30°,65. 使用家用燃气灶烧开同一壶水所需的燃气量 (单位: )与旋钮的旋转角度 (单位:度)( )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度 与燃气量 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )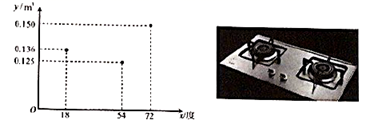 A、 B、 C、 D、6. 已知二次函数 的图象与 轴的一个交点为(-1, 0),则关于 的一元二次方程 的两实数根是( )A、 B、 C、 D、7. 如图, 为 的直径,点 , 在 上.若 ,则 的度数为( )
A、 B、 C、 D、6. 已知二次函数 的图象与 轴的一个交点为(-1, 0),则关于 的一元二次方程 的两实数根是( )A、 B、 C、 D、7. 如图, 为 的直径,点 , 在 上.若 ,则 的度数为( ) A、72° B、54° C、45° D、36°8. 我们把宽与长的比值等于黄金比例 的矩形称为黄金矩形.如图,在黄金矩形 ( )的边 上取一点 ,使得 ,连接 ,则 等于( )
A、72° B、54° C、45° D、36°8. 我们把宽与长的比值等于黄金比例 的矩形称为黄金矩形.如图,在黄金矩形 ( )的边 上取一点 ,使得 ,连接 ,则 等于( ) A、 B、 C、 D、9. 如图,已知正方形 的边长为2,点 是正方形内部一点,连接 , 满足 ,点 是 边上一动点,连结 , .则 长度的最小值为( )
A、 B、 C、 D、9. 如图,已知正方形 的边长为2,点 是正方形内部一点,连接 , 满足 ,点 是 边上一动点,连结 , .则 长度的最小值为( ) A、 B、 C、 D、10. 如图,在 中, 是边 上的点, 是边 上的点,且 , ,若 的面积为1,则 的面积为( )
A、 B、 C、 D、10. 如图,在 中, 是边 上的点, 是边 上的点,且 , ,若 的面积为1,则 的面积为( )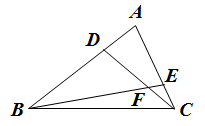 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知 ,则 .12. 一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则摸出2个红球的概率是.13. 在由边长为1的小正方形所组成的网格中, 如图放置,则 .
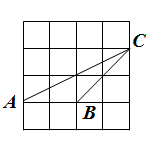 14. 在 中, , , ,点 是该三角形边上一点,且 ,以 为圆心,1为半径作圆,点 是这个圆上的一动点,连接 ,则线段 的最大值为.15. 已知自变量为 的二次函数 经过 、 两点,若方程 的一个根为 ,则其另一个根为.16. 如图,四边形 中, , 平分 , , ,则 的长是 .
14. 在 中, , , ,点 是该三角形边上一点,且 ,以 为圆心,1为半径作圆,点 是这个圆上的一动点,连接 ,则线段 的最大值为.15. 已知自变量为 的二次函数 经过 、 两点,若方程 的一个根为 ,则其另一个根为.16. 如图,四边形 中, , 平分 , , ,则 的长是 .
三、解答题
-
17.(1)、计算:(2)、将 的图象先向左平移2个单位,再向下平移1个单位,求两次平移后所得到的抛物线解析式.18. 如图, , , , 四张卡片上分别写有 四个实数,从中任取两张卡片.
 (1)、用适当的方法列举出所有可能的结果(用字母 , , , 表示)(2)、求取到卡片上的两个数都是无理数的概率.19. 如图, 的半径为2, 是 的弦,点 到弦 的距离为 .
(1)、用适当的方法列举出所有可能的结果(用字母 , , , 表示)(2)、求取到卡片上的两个数都是无理数的概率.19. 如图, 的半径为2, 是 的弦,点 到弦 的距离为 .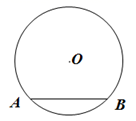 (1)、求弦 的长;(2)、若点C在 上(点C不与A,B重合),求 的度数.20. 如图,三个景点A,B,C之间各建有笔直的健身小道.经测量,景点B在景点A的正东方向,景点C在景点A北偏东60°的方向上,同时也在景点B北偏东45°的方向上,已知 .“运动达人”小敏从景点C出发,沿着 的路径健步走到景点B,景点A,再回到景点C.
(1)、求弦 的长;(2)、若点C在 上(点C不与A,B重合),求 的度数.20. 如图,三个景点A,B,C之间各建有笔直的健身小道.经测量,景点B在景点A的正东方向,景点C在景点A北偏东60°的方向上,同时也在景点B北偏东45°的方向上,已知 .“运动达人”小敏从景点C出发,沿着 的路径健步走到景点B,景点A,再回到景点C.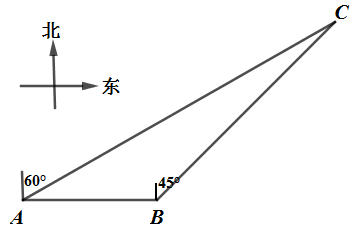
求:
(1)、景点A,B间的距离;(2)、小敏健步走的总路程.21. 现有成135°角且足够长的墙角和可建总长为15m围墙的建筑用料来修建储料场.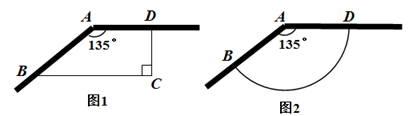 (1)、如图1,修建成四边形ABCD的一个储料场,使 , .新建围墙为BCD.怎样修建围墙才能使储料场的面积最大?最大面积是多少?(2)、爱动脑筋的小聪建议:把新建的围墙建成如图2所示的以A为圆心的圆弧BD,这样修建的储料场面积会更大.聪明的你认为小聪的建议合理吗?请说明理由.22. 如图, 是 的直径, , 是 延长线上一点,且 ,过点 作一直线,分别交 于C,D两点,已知 .
(1)、如图1,修建成四边形ABCD的一个储料场,使 , .新建围墙为BCD.怎样修建围墙才能使储料场的面积最大?最大面积是多少?(2)、爱动脑筋的小聪建议:把新建的围墙建成如图2所示的以A为圆心的圆弧BD,这样修建的储料场面积会更大.聪明的你认为小聪的建议合理吗?请说明理由.22. 如图, 是 的直径, , 是 延长线上一点,且 ,过点 作一直线,分别交 于C,D两点,已知 . (1)、求CD与PC的长;(2)、连结BC,AD,求圆内接四边形ABCD的面积.23. 在平面直角坐标系 中, 的半径为 ,给出如下定义:若点 的横、纵坐标均为整数,且到圆心 的距离 ,则称点 为 的“圈内整点”.
(1)、求CD与PC的长;(2)、连结BC,AD,求圆内接四边形ABCD的面积.23. 在平面直角坐标系 中, 的半径为 ,给出如下定义:若点 的横、纵坐标均为整数,且到圆心 的距离 ,则称点 为 的“圈内整点”. (1)、当 的半径 时,在点 , , , 中,属于 “圈内整点”的是;(2)、若直线 上存在 的“圈内整点”,且不超过8个,求 半径 的取值范围;(3)、 的圆心在 轴上,半径为2,若直线 上存在 的“圈内整点”,求圆心 横坐标 的取值范围.24. 如图1,在平面直角坐标系中,已知点 , ,以 为直径作 ,交 轴的正半轴于点C,连结AC、BC,过A、B、C三点作抛物线.
(1)、当 的半径 时,在点 , , , 中,属于 “圈内整点”的是;(2)、若直线 上存在 的“圈内整点”,且不超过8个,求 半径 的取值范围;(3)、 的圆心在 轴上,半径为2,若直线 上存在 的“圈内整点”,求圆心 横坐标 的取值范围.24. 如图1,在平面直角坐标系中,已知点 , ,以 为直径作 ,交 轴的正半轴于点C,连结AC、BC,过A、B、C三点作抛物线.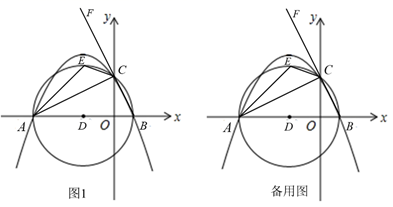 (1)、求抛物线的解析式;(2)、点F是BC延长线上一点, 的平分线CE交 于点E,求点E的坐标;(3)、在(2)的条件下,连结AE,在 上是否存在点P,使得 ?如果存在,请求出点P的坐标;如果不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点F是BC延长线上一点, 的平分线CE交 于点E,求点E的坐标;(3)、在(2)的条件下,连结AE,在 上是否存在点P,使得 ?如果存在,请求出点P的坐标;如果不存在,请说明理由.